NP-complete な問題となかよく - えびちゃんの日記

NP-complete や NP-hard のような概念は、競プロ文脈ではあまり重要視されることがない気がします。多項式時間で解くのが厳しそうな問題が $n\le 20$ 程度の制約で出題されることはあっても、それが実際に NP-hard であることを示す必要は別にありません（示す旨味も特にない気がします）。「NP 問題だから解くのが難しい」のような表現をしている人をしばしば見かけたりもしますし、あまりきちんと理解している人は多くないような印象があります。

それはそれとして、知っている人はちゃんと知っている分野だとも思いますし、一生知らないまま生きるのは嫌だな〜と思ったので調べようと思いました。競プロ文脈でも、「この（言い換えた）問題が解けさえすれば AC なんだけどな」といった状況で、その問題が NP-complete であることを示せれば・知っていれば「この方針だときつくない？」と気づいて別の方針を考えやすくなったりします*1。

disclaimer: 気ままに調べて気ままに書いていたところ、8.3 万文字を超えていました。

用語
帰着①
帰着②
おまけ
- TM からの帰着
あとがき
参考文献
おわり

用語

問題

$\gdef\sol{\operatorname{sol}}$

問題 (problem) は $P = (I, O, \sigma)$ の $3$ つ組であって、次を満たすものとします。

$I$ は入力 (input) 全体からなる集合である。
$O$ は出力 (output) 全体を含む集合である。
$\sigma \colon I \to 2^O$ は解 (solution) 全体からなる集合を与える関数である。

$I$ の各元のことを $P$ の 問題例 (instance) とも呼びます。アルゴリズムによって問題 $P$ を解く (solve) とは、任意の問題例 $\phi\in I$ を入力として受け取り、その解の集合 $\sigma(\phi)$ が空でないならばそのいずれかの元を出力し、空ならばその旨を報告することを指します。

例

数列から偶数を見つける問題 $P$ を考えてみましょう。$I = \Z^{\ast}$ かつ $O = \Z$ とします。解は、その列に含まれる偶数です。

たとえば、$\phi_1 = (1, 4, 2, 8, 5, 7, 1, 4)$ のとき $\sigma(\phi_1) = \{2, 4, 8\}$ です。また、$\phi_2 = (9, 17)$ や $\phi_3 = ()$ に対しては $\sigma(\phi_2) = \sigma(\phi_3) = \emptyset$ です。$\eod$

$\gdef\Yes{\textsc{yes}}$ $\gdef\No{\textsc{no}}$

決定問題 または 判定問題 (decision problem) は、各問題例に対応する解の集合が $\{\Yes\}$ または $\{\No\}$ であるような問題のことを指します。 $\sigma(\phi) = \{\Yes\}$ となる問題例 $\phi\in I$ を Yes-instance と呼び、問題 $P$ の Yes-instance 全体からなる集合を $P_{\Yes}$ と書くことにします。No-instance や $P_{\No}$ についても同様に定義します。

例

数列がソートされているかを決定する問題を考えてみましょう。$I = \Z^{\ast}$ かつ $O = \{\Yes, \No\}$ です。

たとえば、$\phi_1 = (2, 3, 4, 6, 9)$ や $\phi_2 = ()$ に対して $\sigma(\phi_1) = \sigma(\phi_2) = \{\Yes\}$ で、$\phi_3 = (5, 2, 3)$ に対して $\sigma(\phi_3) = \{\No\}$ です。よって、$\phi_1, \phi_2 \in P_{\Yes}$ かつ $\phi_3\in P_{\No}$ です。$\eod$

問題 $P$ を問題 $Q$ に 帰着する (reduce) とは、問題 $Q$ を解くアルゴリズムをサブルーチンとして用いて、問題 $P$ を解くアルゴリズムを構成することを指します。ここでは、決定問題 $P$ に対する問題例 $\phi$ を受け取って決定問題 $Q$ に対する問題例 $\theta$ を出力するような帰着の仕方を主に考えるものとします。ここで、$\phi$ が $P$ の Yes-instance ならば $\theta$ は $Q$ の Yes-instance であり、No-instance ならば No-instance となります。

例

二つの整数が等しいかを決定する問題 $P$ を考えてみましょう。$I_P = \Z^2$ です。たとえば、$(5, 5) \in P_{\Yes}$ で $(2, 4) \in P_{\No}$ です。

ここで、整数が $0$ と等しいかを決定する問題 $Q$ を考えてみます。$I_Q = \Z$ です。$Q_{\Yes} = \{0\}$ で $Q_{\No} = \Z\smallsetminus\{0\}$ です。 $(x, y) \in I_P$ に対して $x-y \in I_Q$ を考えることで、$P$ を $Q$ に帰着できたことになります。$\eod$

Turing 機械

$\gdef\blank{\square}$

Turingチューリング機械 (Turing machine; TM) は、$M = (Q, \Sigma, \Gamma, \delta, \blank, q_0, F)$ の $7$ つ組であって、次の条件を満たすものを指します。

$Q$ は状態 (state) の集合で、空でない有限集合である。
$\Sigma$ は 入力記号 (input symbol) からなる空でない有限集合であり、入力アルファベット (input alphabet) と呼ぶ。
$\Gamma\supset\Sigma$ は テープ記号 (tape symbol) からなる空でない有限集合であり、テープアルファベット (tape alphabet) と呼ぶ。
$\delta\colon (Q\smallsetminus F)\times \Gamma \rightharpoonup Q\times \Gamma \times \{-1, 1\}$ は 遷移関数 (transition function) である。
$\blank\in\Gamma\smallsetminus\Sigma$ は 空白記号 (blank symbol) である。
$q_0\in Q$ は 初期状態 (initial state) である。
$F\subseteq Q$ は 受理状態 (accepting state) である。

ここで、$A\rightharpoonup B$ は $A$ から $B$ への 部分関数 (partial function) で、任意の $a\in A$ に対して $f(a)$ は未定義であるか $f(a)\in B$ であることを意味します。

TM $M$ に対して文字列 $w\in \Sigma^{\ast}$ を与えることを考えます。このとき、$M$ は以下に示す手順に従って $w$ を 受理する (accepts) か、拒否する (rejects) か、停止しない (does not halt) かのいずれかになります。 $M$ が受理する文字列全体からなる集合を $L(M)$ と書きます。

note: 「停止する」は「受理する」または「拒否する」と同じです。「受理しない」は「拒否する」または「停止しない」と同じです。

上記の $Q$ の要素であるところの状態に加え、テープ (tape) と ヘッド (head) という概念を考えます。テープは、テープ記号からなる無限列です。$M$ に $w = w_0\dots w_{n-1}$ を与えたとき、テープは初め $T = (w_0, \dots, w_{n-1}, \blank, \blank, \dots)$ です。ヘッドはテープのいずれかの場所を指しています。初めはテープの $0$ 番目（最も左、$w_0$ のある位置）を指します。また、初めの状態は初期状態 $q_0$ です。

すなわち、一番最初のイメージ図は次のような感じです。 $$ \begin{aligned} q_0; &&& (w_0, w_1, \dots, w_{n-1}, \blank, \blank, \dots) \\ &&& \;\uarr \end{aligned} $$ さて、状態が $q$ であり、かつヘッドがテープの $i$ 番目の文字 $T_i$ を見ているとき、$\delta(q, T_i)$ に応じて遷移します。 $\delta(q, T_i)$ が未定義のとき、$M$ は $w$ を拒否します。 $\delta(q, T_i) = (q', c, \Delta i)$ のとき、$T_i \gets c$ で書き換え、状態を $q'$ にし、$i \xgets{+} \Delta i$ で更新します*2。テープのうちヘッドがいない場所にある文字は書き変わりません。

たとえば、$\delta(q_0, w_0) = (q_1, \blank, 1)$ だった場合、上図の状態から次のように遷移します。 $$ \begin{aligned} q_1; &&& (\blank, w_1, \dots, w_{n-1}, \blank, \blank, \dots) \\ &&& \;\hphantom{\blank, \,}\uarr \end{aligned} $$

これを繰り返し、状態 $q$ が $q\in F$ になったら $M$ は $w$ を受理します。有限回の遷移では受理も拒否もしないとき、停止しないと言います。

TM $M$ が、長さ $n$ の任意の文字列 $w\in\Sigma^n$ に対して $t(n)$ ステップで停止するとき、$M$ は $t(n)$ time-bounded であると言います。同様に、停止するまでのヘッドの位置の最大値が $s(n)$ であるとき $M$ は $s(n)$ tape-bounded であると言います。

符号化

問題を TM によって解くことを考えます。グラフなどを直接与えることはできないので、$\Sigma$ 上の文字列として 符号化する (encode) ことを考えます。何らかの対象 $\phi$ を符号化したものを $\angled{\phi}$ と書きます。$\angled{(\phi, \theta, \dots)}$ を単に $\angled{\phi, \theta, \dots}$ と書くことにします。

符号化方式 (encoding) は、その文脈において適切であればなんでもいいと思います。

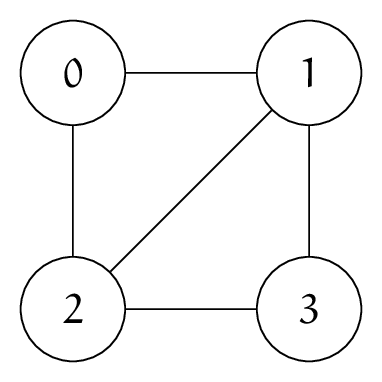
たとえば、以下のようなグラフ $G$ を考えます。

AtCoder でよくある入力形式では次のようになります。頂点数 $n$ と辺の本数 $m$ を最初に書き、その後に辺を持つペアを列挙する形式ですね。

あるいは、次のような場合もあるでしょう。

$\Sigma = \{0, 1, \#\}$ とし、たとえば $$ \angled{G} = 1111\#100\#0\#1\#0\#10\#1\#10\#1\#11\#10\#11 $$ のようなものが考えられます。頂点数の個数だけ $1$ を並べ、残りの数は $2$ 進法で $\#$ 区切りで並べています。

事情

頂点数 $n$ を $2$ 進法で並べると、たとえば辺が $0$ 本のとき $\Theta(\log(n) )$ 程度の長さになります。これに対して $\Theta(n)$ 時間のアルゴリズムを走らせると $|\angled{\phi}|$ に対して指数的な時間がかかることになって不都合だな〜という気がしたので、頂点数に関してはそういう符号化をしました。 $|\angled{\phi}| \ge n$ であれば、$n^{\Theta(1)} \in |\angled{\phi}|^{O(1)}$ になるので、助かる気がします。$\eod$

あるいは、隣接行列をイメージして $$ \angled{G} = 0110\#1011\#1101\#0110 $$ のようにする方法もありでしょう。

嘘を書いたので折りたたみました

他にも、たとえば、$2^{|V|} \cdot \prod {\{3^{i |V|+j} \mid \{i, j\}\in E\}}$ のようにして一つの整数として表す方法も考えられる気がします*3。たとえば、上記のグラフ $G$ に対しては $$ 2^4\cdot 3^{0\cdot4+1}\cdot 3^{0\cdot4+2}\cdot 3^{1\cdot4+2}\cdot 3^{1\cdot4+3}\cdot 3^{2\cdot4+3} = 122009559759792 $$ が成り立ちます。一般の $G = (V, E)$ に対して、この整数の下限は $2^{|V|}$ で、上界は $$ \begin{aligned} 2^{|V|}\cdot \prod_{i=0}^{|V|^2-1} 3^i &= 2^{|V|}\cdot 3^{\sum_{i=0}^{|V|^2-1} i} \\ &= 2^{|V|}\cdot 3^{\tfrac12\cdot |V|^2 (|V|^2-1)}, \\ \log_2\left(2^{|V|}\cdot \prod_{i=0}^{|V|^2-1} 3^i\right) &= |V| + \frac{\log_23}2\cdot |V|^2 (|V|^2-1) \end{aligned} $$ なので、この整数を $2$ 進法などで書けば $|V|^{\Theta(1)}$ 桁になります。うれしいかは文脈によりますね*4。$\eod$

TM $D$ が決定問題 $P$ を解くというのは、任意の $w\in\Sigma^{\ast}$ に対して $D$ は停止し、また $L(D) = \{\angled{\phi} \mid \phi \in P_{\Yes}\}$ が成り立つのに相当します。こうした $D$ のことを $P$ の 決定器 (decider) と言います。停止するとは限らないが $L(M) = \{\angled{\phi} \mid \phi \in P_{\Yes}\}$ なる TM $M$ のことは $P$ の 認識器 (recognizer) と言います*5。

人間視点だと、$P$ の決定器を構成しましょうという遊びですね。

「任意の決定問題について決定器が存在するか？」とか「任意の決定問題について認識器が存在するか？」とかの話は、別の記事で書くかもしれないし書かないかもしれません。

NP 問題

$\gdef\P{\textsf{P}}$ $\gdef\NP{\textsf{NP}}$ $\gdef\NTIME{\textsf{NTIME}}$

$\NP$ はある種の決定問題からなる集合です。

本来っぽい定義

非決定性 Turing 機械というのを別途定義する必要があります。Turing 機械における遷移関数が遷移関係になって、受理の条件にも手が加わったものです。遷移の仕方が一意ではなくなり、「どれか好きなように遷移できる」「遷移の仕方をうまく選ぶことで受理状態に到達できるなら受理する」といった具合です。

入力の長さが $n$ のときにこの機械を用いて $O(f(n))$ ステップで解ける決定問題全体からなる集合を $\NTIME(f(n) )$ と書きます。

これを用いて、$\NP = \bigcup_{k\in\N} \NTIME(n^k)$ と定義されます。$\eod$

任意の問題 $P\in\NP$ に対し*6、TM $V$、集合 $C$、多項式 $p$ であって下記を満たすものが存在します*7。

任意の $\phi\in P_{\Yes}\cup P_{\No}$ と $c\in C$ に対し、$V$ は $\angled{\phi, c}$ を与えたとき高々 $p(|\angled{\phi}|)$ ステップで停止する。
$\phi\in P_{\Yes}$ ならば、ある $c\in C$ が存在し、$V$ は $\angled{\phi, c}$ を受理する。
- このような $c$ を $\phi$ に対する証拠 (certificate, witness) と呼ぶ。
$\phi\in P_{\No}$ ならば、任意の $c\in C$ に対し、$V$ は $\angled{\phi, c}$ を拒否する。

note: 下二つの条件を満たす決定器を $P$ の 検証器 (verifier) と言います。$\NP$ に属する問題に対しては、多項式時間で停止する検証器が常に存在するということですね。

例については、次の章で $\NP$ の問題を導入したときに併せて挙げます。

NP-complete

問題 $P$ が NP-hard であるとは、任意の $Q\in\NP$ が $P$ に多項式時間で帰着できることを指します。問題 $P$ が NP-complete であるとは、$P\in\NP$ かつ $P$ が NP-hard であることを指します。

多項式時間で解くことができる問題全体からなる集合を $\P$ と書きますが、$\P$ に属する問題は当然多項式時間で検証できる（検証と言いつつふつうに解いてしまっても多項式時間しかかからない）ので $\P\subseteq\NP$ です。そのため、$P\in\NP$ だけ示しても NP-complete かどうかはわからず、「NP 問題なので難しい」はあまり妥当でない主張な気がします。 $\NP$ の中には全然簡単な問題も属しているので、それと区別した言い方になっていないということですね。

帰着①

各節では、問題の紹介をはじめに行い、別の NP-complete な問題から帰着できることを示します。帰着の証明では、まず別の NP-complete な問題の問題例 $\phi$ から、その問題の問題例 $\theta$ を構成する方法を述べます。その後、$\phi$ が Yes-instance であることと $\theta$ が Yes-instance であることの同値性を示します。典型的には、$\phi$ の certificate を用いて $\theta$ の certificate を構成できることと、その逆方向をそれぞれ示すことになります。

なお、$\theta$ の構成が $|\angled{\phi}|$ に対して多項式ステップでできることも示す必要があります。 $|\angled{\theta}| \in |\angled{\phi}|^{O(1)}$ であることが必要になると思います。

添字の集合を表すときに便利なので、非負整数 $k$ に対して $\Lambda_k = \{0, 1, \dots, k-1\}$ と定義します。

CNF Satisfiability (CNF SAT)

まずは、実際に NP-complete である問題が実際に存在することを示します。

$n$ 個の変数 $x_0, \dots, x_{n-1}\in\{0, 1\}$ からなる論理式 $$ \begin{aligned} \phi &= \bigwedge_{i=0}^{m-1} \bigvee_{j=0}^{k_i-1} \alpha_{i, j} \\ &= (\alpha_{0, 0}\vee\dots\vee\alpha_{0, k_0-1})\wedge\dots\wedge(\alpha_{m-1, 0}\vee\dots\vee\alpha_{m-1, k_{m-1}-1}) \end{aligned} $$ が与えられます。ここで、$\alpha_{i, j}$ は $x_0, \lnot x_0, \dots, x_{n-1}, \lnot x_{n-1}$ のいずれかです。このとき、$\bm{x} = (x_0, \dots, x_{n-1}) \in \{0, 1\}^n$ であって $\phi(\bm{x}) = 1$ なるものが存在するか？という問題です。なお、その $\bm{x}$ が存在するとき、$\phi$ は 充足可能である (is satisfiable) と言います*8。

note: CNF は 連言れんげん標準形 (conjunctive normal form) の略で、$\bigwedge\bigvee\alpha$ の形の論理式のことです。 $\bigvee\bigwedge\alpha$ の形の論理式は 選言せんげん標準形 (disjunctive normal form, DNF) と呼ばれます。

各 $\bigvee \alpha$ のことを節 (clause) と呼びます。また、各 $\alpha$ のことを リテラル (literal) と呼びます。

各演算子の定義は次の通りです。 $$ \begin{aligned} \def\arraystretch{1.5} \begin{array}{c|c:c} \vee & 0 & 1 \\ \hline 0 & 0 & 1 \\ \hdashline 1 & 1 & 1 \end{array} \qquad\quad \def\arraystretch{1.5} \begin{array}{c|c:c} \wedge & 0 & 1 \\ \hline 0 & 0 & 0 \\ \hdashline 1 & 0 & 1 \end{array} \qquad\quad \def\arraystretch{1.5} \begin{array}{c|c:c} \lnot & 0 & 1 \\ \hline & 1 & 0 \end{array} \end{aligned} $$ また、$\{0, 1\}\times\{0, 1\}\to\{0, 1\}$ の演算として次のものも導入しておきます。 $$ \begin{aligned} \def\arraystretch{1.5} \begin{array}{c|c:c} \rarr & 0 & 1 \\ \hline 0 & 1 & 1 \\ \hdashline 1 & 0 & 1 \end{array} \qquad\quad \def\arraystretch{1.5} \begin{array}{c|c:c} \harr & 0 & 1 \\ \hline 0 & 1 & 0 \\ \hdashline 1 & 0 & 1 \end{array} \end{aligned} $$ $\rarr$ は $1\rarr 0$ のみが $0$ で、それ以外の組合せでは $1$ となります。$x\rarr y = \lnot x\vee y$ や $x\harr y = (x\rarr y)\wedge(y\rarr x)$ が成り立ちます。これを用いると SAT は $$ \bigwedge_{i=0}^{m-1}\bigvee_{j=0}^{k_i-1} \alpha_{i, j} = \bigwedge_{i=0}^{m-1}\bigvee_{j=0}^{k_i-1} {(x_{l_{i, j}} \harr a_{i, j})} $$ のような形で書くことができます。ここで $l_{i, j}\in \Lambda_n$ かつ $a_{i, j}\in\{0, 1\}$ です。

例

$\phi = (x_0\vee x_1)\wedge(\lnot x_0\vee \lnot x_1\vee x_2) \wedge (x_0\vee \lnot x_2)$ とすると、$\bm{x} = (x_0, x_1, x_2) = (1, 0, 0)$ に対して $\phi(\bm{x}) = 1$ となります。このような $\bm{x}$ を探すのは一般には難しいですが、固定された $\bm{x}$ に対して $\phi(\bm{x})$ を計算することは容易です。自然な検証器としては、この $\bm{x}$ を certificate として使うものが考えられます。

また、$\psi = (x_0)\wedge(\lnot x_0)$ とすると $\psi(\bm{x}) = 1$ なる $\bm{x}$ は存在しません。$\eod$

Claim 1: CNF SAT は任意の $P\in\NP$ から多項式時間で帰着できる。

Proof

任意の $P\in\NP$ を固定する。ある多項式 $t$, $s$ が存在し、$P$ の $t(n)$ time-bounded, $s(n)$ tape-bounded な検証器 $V = (Q, \Sigma, \Gamma, \delta, \blank, q_0, F)$ が存在する。

ここで $q_{\text{reject}}\notin Q$ を用いて $Q' = Q\cup \{q_{\text{reject}}\}$ とし、$\delta'\colon Q'\times \Gamma\to Q'\times\Gamma\times \{-1, 0, 1\}$ を次のように定義する。 $$ \delta'(q, c) = \begin{cases} (q', c', \Delta j), & \text{if}\; \delta(q, c) = (q', c', \Delta j); \\ (q, c, 0), & \text{if}\; q\in F; \\ (q_{\text{reject}}, c, 0), & \text{otherwise}. \end{cases} $$

$P$ の問題例 $\phi$ に対し、$w = \angled{\phi}$ かつ $|w| = n$ とする。テープの長さを $s(n)$ とし、テープの初期値を $$ (w_0, \dots, w_{n-1}, T_n, \dots, T_{s(n)-1}) $$ とする。ここで、$T_n, \dots, T_{s(n)-1} \in \Gamma$ である。$V$ の条件より、これを $t(n)$ ステップで受理することと $\phi\in P_{\Yes}$ であることは同値である。

次に示す $(t(n)+1)\cdot(|Q'| + (s(n)+1) + s(n) |\Gamma|)$ 個の変数を用いた CNF SAT $P'$ の問題例 $\theta$ に対し、$\phi\in P_{\Yes} \iff \theta \in P'_{\Yes}$ となることを示す。

$x_{i, q}^{\text{state}}$ は、$i$ 回の遷移の後の状態が $q$ であることと同値とする。
- $i\in\Lambda_{t(n)+1}$
- $q \in Q'$
$x_{i, j}^{\text{head}}$ は、$i$ 回の遷移の後のヘッドの位置が $j$ であることと同値とする。
- $i\in\Lambda_{t(n)+1}$
- $j\in\Lambda_{s(n)}\cup\{-1\}$
$x_{i, j, c}^{\text{symbol}}$ は、$i$ 回の遷移の後のテープの $j$ 番目の文字が $c$ であることと同値とする。
- $i\in\Lambda_{t(n)+1}$
- $j\in\Lambda_{s(n)}$
- $c\in\Gamma$

これは、次のようにして表現できる。

$$ \begin{aligned} \theta &= x_{0, q_0}^{\text{state}} \wedge x_{0, 0}^{\text{head}} \wedge \bigwedge_{j=0}^{n-1} x_{0, j, w_j}^{\text{symbol}} \wedge \left(\bigvee_{q\in F} x_{t(n), q}^{\text{state}}\right) \\ & \qquad\quad {} \wedge \bigwedge_{j=n}^{s(n)-1} \bigwedge_{c\in\Gamma\smallsetminus(\Sigma\cup\{\blank\})} \lnot x_{0, j, c}^{\text{symbol}} \wedge \bigwedge_{j=n+1}^{s(n)-1} (x_{0, j-1, \blank}^{\text{symbol}}\to x_{0, j, \blank}^{\text{symbol}}) \\ & \qquad\quad {} \wedge \bigwedge_{i=0}^{t(n)} \left(\sum_{q\in Q'} x_{i, q}^{\text{state}} = 1\right) \wedge \bigwedge_{i=0}^{t(n)} \bigwedge_{j=0}^{s(n)-1} \left(\sum_{c\in\Gamma} x_{i, j, c}^{\text{symbol}} = 1\right) \\ & \qquad\quad {} \wedge \bigwedge_{i=0}^{t(n)} \left(\sum_{j=0}^{s(n)-1} x_{i, j}^{\text{head}} = 1\right) \wedge \bigwedge_{i=0}^{t(n)} \lnot x_{i, -1}^{\text{head}} \\ & \qquad\quad {} \wedge \bigwedge_{i=0}^{t(n)-1} \bigwedge_{j=0}^{s(n)-1} \bigwedge_{\delta'(q, c)=(q', c', \Delta j)} \left( (x_{i, q}^{\text{state}}\wedge x_{i, j}^{\text{head}}\wedge x_{i, j, c}^{\text{symbol}})\to x_{i+1, q'}^{\text{state}} \right) \\ & \qquad\quad {} \wedge \bigwedge_{i=0}^{t(n)-1} \bigwedge_{j=0}^{s(n)-1} \bigwedge_{\delta'(q, c)=(q', c', \Delta j)} \left( (x_{i, q}^{\text{state}}\wedge x_{i, j}^{\text{head}}\wedge x_{i, j, c}^{\text{symbol}})\to x_{i+1, j+\Delta j}^{\text{head}} \right) \\ & \qquad\quad {} \wedge \bigwedge_{i=0}^{t(n)-1} \bigwedge_{j=0}^{s(n)-1} \bigwedge_{\delta'(q, c)=(q', c', \Delta j)} \left( (x_{i, q}^{\text{state}}\wedge x_{i, j}^{\text{head}}\wedge x_{i, j, c}^{\text{symbol}})\to x_{i+1, j, c'}^{\text{symbol}} \right) \\ & \qquad\quad {} \wedge \bigwedge_{i=0}^{t(n)-1} \bigwedge_{j=0}^{s(n)-1} \bigwedge_{(q, c)\in Q'\times\Gamma} \left( (x_{i, q}^{\text{state}}\wedge \lnot x_{i, j}^{\text{head}}\wedge x_{i, j, c}^{\text{symbol}})\to x_{i+1, j, c}^{\text{symbol}} \right). \end{aligned} $$ ここで、 $$ \begin{aligned} \left(\sum_{x\in S} x = 1\right) &= \left(\bigvee_{x\in S} x\right) \wedge \left(\bigwedge_{x\in S\mathstrut} \bigwedge_{x'\in S\smallsetminus\{x\}} \lnot (x\wedge \lnot x')\right) \\ &= \left(\bigvee_{x\in S} x\right) \wedge \left(\bigwedge_{x\in S\mathstrut} \bigwedge_{x'\in S\smallsetminus\{x\}} (\lnot x\vee \lnot x')\right) \\ \left(\bigwedge_{x\in S} x\right)\to y &= \left(\bigvee_{x\in S} \lnot x\right)\vee y \end{aligned} $$ が成り立つため、$\theta$ は CNF SAT の instance として表せる。

任意の $x_{i, q}^{\text{state}}, x_{i, j}^{\text{head}}, x_{i, j, c}^{\text{symbol}}$ が定まっているとき、$\delta'$ の遷移に対応するように $x_{i+1, q}^{\text{state}}, x_{i+1, j}^{\text{head}}, x_{i+1, j, c}^{\text{symbol}}$ を定めないと $\theta(\bm{x}) = 0$ となることに注意せよ。

$\phi\in P_{\Yes}$ ならば、ある $T_n, \dots, T_{s(n)-1}$ が存在して $(w_0, \dots, w_{n-1}, T_n, \dots, T_{s(n)-1})$ を $V$ が受理するため、$V$ の遷移に応じて $\bm{x}$ を定めることで $\theta(\bm{x}) = 1$ となる。特に、$\bigvee_{q\in F} x_{t(n), q}^{\text{state}} = 1$ となることに注意せよ。

逆に、$\theta\in P'_{\Yes}$ ならば、$(T_n, \dots, T_{s(n)-1}) = (c_n, \dots, c_{n+|c|-1}, \blank, \dots, \blank)$ となるような $c = c_n\dots c_{n+|c|-1}\in\Sigma^{\ast}$ が得られる。これが $\phi$ に対する certificate となるため、$\phi\in P_{\Yes}$ となる。$\qed$

帰着の具体例は、後に紹介する NP-complete な問題のうち、検証器を簡単に構成できるものを用いて後半で示します。

Circuit Satisfiability (Circuit SAT)

$n+m$ 個の変数 $x_0, \dots, x_{n+m-1}\in\{0, 1\}$ が与えられます。ただし、各 $i\in\Lambda_m$ について $n+i$ 番目の変数は次のいずれかの形で与えられます。

$x_{n+i} = 0$
$x_{n+i} = 1$
$x_{n+i} = \lnot x_j$
$x_{n+i} = x_j \wedge x_k$
$x_{n+i} = x_j \vee x_k$

ただし、$j, k\in \Lambda_{n+i}$ とします。このとき、$\bm{x} = (x_0, \dots, x_{n-1})$ であって $m$ 個の方程式を満たしつつ $x_{n+m-1} = 1$ なるものが存在するか？という問題です。

note: 与えられた 論理回路 (Boolean circuit) の出力を $1$ にするような入力が存在するか？というのに対応しています。

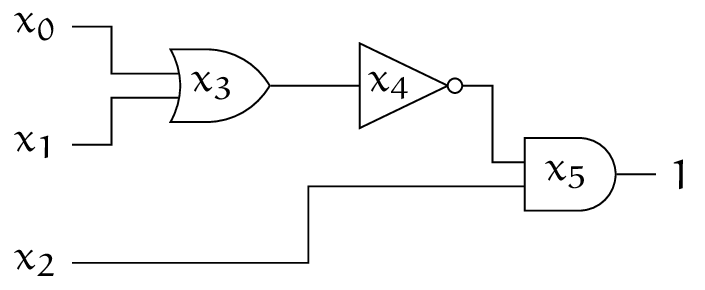
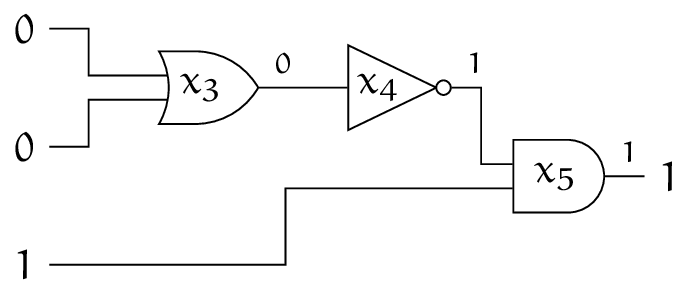
例

$n = 3$, $m = 3$ で $$ \begin{aligned} x_3 &= x_0 \vee x_1, \\ x_4 &= \lnot x_3, \\ x_5 &= x_2 \wedge x_4 \end{aligned} $$ となる回路です。$\bm{x} = (0, 0, 1)$ とすることで条件を満たすことができます。

よって、上記の $\phi$ は Yes-instance であることがわかります。$\eod$

Claim 2: Circuit SAT は SAT から多項式時間で帰着できる。

Proof

SAT の問題例を $$ \phi = \bigwedge_{j=0}^{m-1} \bigvee_{k=0}^{c_j-1} {(x_{l_{j, k}}\harr a_{j, k})} $$ とし、各 $j$, $k$ について $l_{j, k}\in\Lambda_n$ かつ $a_{j, k}\in\{0, 1\}$ とする。すなわち、変数を $n$ 個とする。ここで、$c_j\le |\Lambda_n\times\{0, 1\}|=2n$ としても一般性を失わない。

便宜上、各 $j\in\Lambda_{m+1}$ に対して $s_j = \sum_{k=0}^{j-1} c_j$ とする。$s_m\le 2mn$ が成り立つ。

$2n+s_m$ 個の変数の Circuit SAT に帰着できる。まず、各 $i\in\Lambda_n$ に対して $x_{n+i} = \lnot x_i$ とする。 $x_{2n}=1$ とし、各 $j\in\Lambda_m$ と $k\in\Lambda_{c_j-2}$ に対して $$ \begin{aligned} x_{2n+s_j+1} &= (x_{(1-a_{j, 0})n+l_{j, 0}}) \vee (x_{(1-a_{j, 1})n+l_{j, 1}}), \\ x_{2n+s_j+k+2} &= (x_{2n+s_j+k+1}) \vee (x_{(1-a_{j, k+2})n+l_{j, k+2}}), \\ x_{2n+s_{j+1}} &= x_{2n+s_j} \wedge x_{2n+s_{j+1}-1} \end{aligned} $$ で定義する。

$x_{2n+s_m} = 1$ と $\phi(\bm x) = 1$ が同値であることは明らか。$\qed$

また、Circuit SAT が NP であることから、Claim 1 より CNF SAT に帰着できることは明らかですが、直接的に帰着できることを示します。

Claim 3: CNF SAT は Circuit SAT から帰着できる。

Proof

Circuit SAT の問題例 $\phi$ において、各 $i\in\Lambda_m$ に対して $x_{n+i} = f_i(x_0, \dots, x_{n+i-1})$ であるとする。このとき、 $$ \theta = x_{n+m-1} \wedge \left(\bigwedge_{i=0}^{m-1} \big(x_{n+i}\harr f_i(x_0, \dots, x_{n+i-1})\big) \right) $$ と定義する。ただし、 $$ \begin{aligned} x_{n+i}\harr 0 &= \lnot x_{n+i}, \\ x_{n+i}\harr 1 &= x_{n+i}, \\ x_{n+i} \harr \lnot x_j &= (x_{n+i} \to \lnot x_j) \wedge (\lnot x_j \to x_{n+i}) \\ &= (\lnot x_{n+i} \vee \lnot x_j) \wedge (x_j\vee x_{n+i}), \\ x_{n+i} \harr (x_j\wedge x_k) &= (x_{n+i} \to (x_j\wedge x_k) ) \wedge ( (x_j\wedge x_k) \to x_{n+i}) \\ &= (\lnot x_{n+i} \vee (x_j\wedge x_k) ) \wedge (\lnot (x_j\wedge x_k) \vee x_{n+i}) \\ &= ( (\lnot x_{n+i} \vee x_j) \wedge (\lnot x_{n+i} \vee x_k) ) \wedge ( (\lnot x_j\vee \lnot x_k) \vee x_{n+i}) \\ &= (x_{n+i}\vee \lnot x_j\vee \lnot x_k) \wedge (\lnot x_{n+i} \vee x_j) \wedge (\lnot x_{n+i} \vee x_k), \\ x_{n+i} \harr (x_j\vee x_k) &= (x_{n+i} \to (x_j\vee x_k) ) \wedge ( (x_j\vee x_k) \to x_{n+i}) \\ &= (\lnot x_{n+i} \vee (x_j\vee x_k) ) \wedge (\lnot(x_j\vee x_k) \vee x_{n+i}) \\ &= (\lnot x_{n+i} \vee (x_j\vee x_k) ) \wedge ( (\lnot x_j\wedge \lnot x_k) \vee x_{n+i}) \\ &= (\lnot x_{n+i} \vee (x_j\vee x_k) ) \wedge ( (\lnot x_j\vee x_{n+i}) \wedge (\lnot x_k\vee x_{n+i}) ) \\ &= (\lnot x_{n+i} \vee x_j\vee x_k) \wedge (x_{n+i}\vee\lnot x_j) \wedge (x_{n+i}\vee\lnot x_k). \end{aligned} $$ に注意する。

よって、変数は $n+m$ 個で、各節内のリテラルの個数の総和は $7m+1$ 個で押さえられる。$\qed$

3-CNF Satisfiability (3-CNF SAT, 3-SAT)

CNF SAT の部分問題であって、各節がちょうど $3$ つの相異なるリテラルで表されるものです*9。

Claim 4: 3-SAT は SAT から帰着できる。

Proof

各節のリテラルが相異なるように重複を除去するのは簡単なので、以下では相異なるものとして考える。

Case 1: $1$ 個のリテラルからなる節 $x_0$

変数 $z_0$, $z_1$ を導入する。 $$ c = (x_0\vee z_0\vee z_1) \wedge (x_0\vee z_0\vee \lnot z_1) \wedge (x_0\vee \lnot z_0\vee z_1) \wedge (x_0\vee \lnot z_0\vee \lnot z_1) $$ とすると、$x_0 = 0$ のとき、 $$ \begin{aligned} c &= (x_0\vee z_0\vee z_1) \wedge (x_0\vee z_0\vee \lnot z_1) \wedge (x_0\vee \lnot z_0\vee z_1) \wedge (x_0\vee \lnot z_0\vee \lnot z_1) \\ &= (z_0\vee z_1) \wedge (z_0\vee \lnot z_1) \wedge (\lnot z_0\vee z_1) \wedge (\lnot z_0\vee \lnot z_1) \\ &= (z_0 \vee (z_1\wedge \lnot z_1) ) \wedge (\lnot z_0\vee z_1) \wedge (\lnot z_0\vee \lnot z_1) \\ &= (z_0 \vee 0) \wedge (\lnot z_0\vee z_1) \wedge (\lnot z_0\vee \lnot z_1) \\ &= 0 \end{aligned} $$ である。また、$x_0 = 1$ のとき明らかに $c = 1$ である。すなわち、任意の論理式 $\psi$ に対して $\psi\wedge x_0$ と $\psi\wedge c$ の充足可能性が同値となる。

よって、変数を $2$ 個、総リテラル数を $11$ 個増やすことで、$3$ 個のリテラルからなる節 $4$ 個に置換できる。

Case 2: $2$ 個のリテラルからなる節 $x_0\vee x_1$

変数 $z_0$ を導入する。 $$ c = (x_0\vee x_1\vee z_1) \wedge (x_0\vee x_1\vee \lnot z_0) $$ とすると、Case 1 同様にして、任意の論理式 $\psi$ に対して $\psi\wedge (x_0\vee x_1)$ と $\psi\wedge c$ の充足可能性が同値となる。

よって、変数を $1$ 個、総リテラル数を $4$ 個増やすことで、$3$ 個のリテラルからなる節 $2$ 個に置換できる。

Case 3: $k$ 個 ($k \gt 3$) のリテラルからなる節 $x_0 \vee \dots \vee x_{k-1}$

変数 $z_0$ を導入する。 $$ c = (x_0 \vee \dots \vee x_{k-3} \vee z_0) \wedge (\lnot z_0 \vee x_{k-2} \vee x_{k-1}) $$ とすると、任意の論理式 $\psi$ に対して $\psi\wedge (x_0\vee \dots \vee x_{k-1})$ と $\psi\wedge c$ の充足可能性が同値となる。

($\implies$): 任意の $\bm x$ に対して、$\psi\wedge(x_0\vee \dots \vee x_{k-1}) = 1$ ならば、ある $z_0$ が存在して $\psi\wedge c = 1$ となることを示す。

$x_0\vee \dots \vee x_{k-1} = 1$ であるから、ある $i$ が存在して $x_i = 1$ が成り立つ。 $i\le k-3$ のとき、$z_0 = 0$ とすることで $c = 1$ が成り立つ。また、$i\gt k-3$ のとき、$z_0 = 1$ とすることで $c = 1$ が成り立つ。

また、$\psi = 1$ であるから、上記の $z_0$ に対して $\psi\wedge c = 1$ となる。

($\impliedby$): 任意の $\bm x$ と $z_0$ に対して、$\psi\wedge c = 1$ ならば ${\psi\wedge (x_0\vee\dots\vee x_{k-1})} = 1$ となることを示す。

$z_0 = 0$ のとき、$x_0\vee\dots\vee x_{k-3} = 1$ なので $x_0\vee\dots\vee x_{k-1} = 1$ が成り立つ。また、$z_0 = 1$ のとき、$x_{k-2}\vee x_{k-1} = 1$ なので $x_0\vee\dots\vee x_{k-1} = 1$ が成り立つ。

さらに $\psi = 1$ であるから、$z_0$ の値によらず $\psi\wedge(x_0\vee\dots\vee x_{k-1}) = 1$ となる。

以上より、任意の論理式 $\psi$ に対して $\psi\wedge (x_0\vee \dots \vee x_{k-1})$ と $\psi\wedge c$ の充足可能性が同値となる。

よって、変数を $1$ 個、総リテラル数を $2$ 個増やすことで、$k-1$ 個のリテラルからなる節と $3$ 個のリテラルからなる節に分解できる。これを繰り返すことにより、変数を $k-3$ 個、総リテラル数を $2(k-3)$ 個増やすことで、$3$ 個のリテラルからなる節 $k-2$ 個に分解できる。

全体として、$k$ 個のリテラルからなる節が $c_k$ 個あるとき、変数の増分は $$ \begin{aligned} 2 c_1 + 1 c_2 + \sum_{i=4}^k {(k-3) c_k} &\le 2\sum_{i=1}^k {k c_k}, \end{aligned} $$ 総リテラル数の増分は $$ \begin{aligned} 11 c_1 + 4 c_2 + \sum_{i=4}^k {2(k-3) c_k} &\le 11\sum_{i=1}^k k c_k, \end{aligned} $$ 節の個数は $$ \begin{aligned} 4 c_1 + 2 c_2 + c_3 + \sum_{i=4}^k {(k-2) c_k} &\le 4\sum_{i=1}^k k c_k \end{aligned} $$ となる。

以上より、$\phi$ の総リテラル数を $l=\sum_k k c_k$ として、$\theta$ は高々 $n+2l$ 変数、高々 $4l$ 個の節で、総リテラル数が高々 $12l$ 個の 3-CNF となる。$\qed$

Maximum Independent Set (MIS)

無向グラフ $G = (V, E)$ が与えられます。$S\subseteq V$ であって、任意の $u, v\in S$ ($u\ne v$) について $\{u, v\}\notin E$ を満たすものを 独立集合 (independent set) と呼びます。要素数が最大となる独立集合（または要素数の最大値）を求めよという問題です。

これは最大化問題であって決定問題ではないですが、決定問題版を「グラフ $G$ と整数 $k$ が与えられる。$|S|\ge k$ なる $S$ が存在するか？」として定義できます。この $k$ について二分探索なり指数探索なりをすることで、（$|S|\le |V|$ に注意して）最大化問題を多項式時間で解くことができます。

例

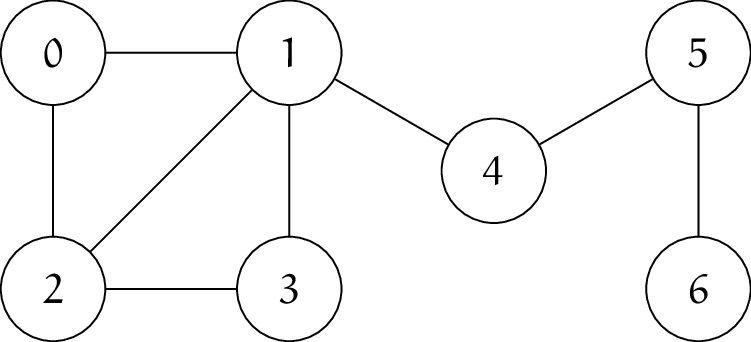
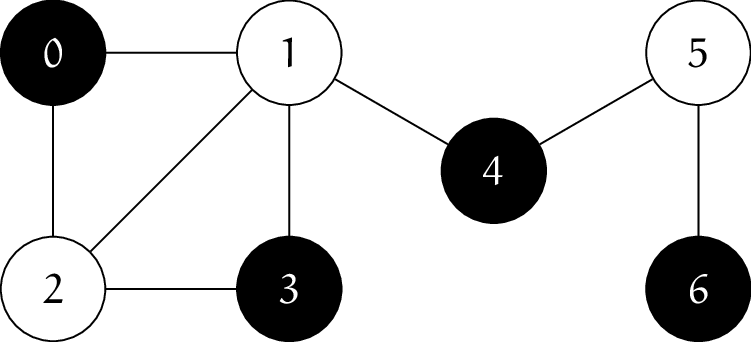
下記のグラフ $G$ に対して、Independent Set の問題例 $\phi = (G, 4)$ を考えます。

次の図で黒く塗った頂点からなる集合 $\{0, 3, 4, 6\}$ は条件を満たします。

よって、上記の $\phi$ は Yes-instance であることがわかります。$\eod$

Claim 5: Independent Set は 3-SAT から帰着できる。

Proof

3-SAT の問題例を $$ \phi = \bigwedge_{j=0}^{m-1} {( (x_{l_{j, 0}} \harr a_{j, 0})\vee(x_{l_{j, 1}} \harr a_{j, 1})\vee(x_{l_{j, 2}} \harr a_{j, 2}) )} $$ とし、変数が $n$ 個であるとする。すなわち、各 $j$ に対して $l_{j, 0}, l_{j, 1}, l_{j, 2}\in\Lambda_n$ であり、$a_{j, 0}, a_{j, 1}, a_{j, 2}\in\{0, 1\}$ とする。各 $i$ に対して $x_i\harr 0$ と $x_i\harr 1$ がそれぞれ $\lnot x_i$ と $x_i$ のリテラルに相当する。

$V = \Lambda_m\times\Lambda_3$ とし、各リテラルが出現する位置の集合を次のように定義する。すなわち、各 $i\in\Lambda_n$ に対し $$ \begin{aligned} S_{\lnot x_i} &= \{(j, k) \in V \mid (l_{j, k}, a_{j, k}) = (i, 0)\}, \\ S_{x_i} &= \{(j, k) \in V \mid (l_{j, k}, a_{j, k}) = (i, 1)\} \end{aligned} $$ とする。これを用いて $$ \begin{aligned} E_{\text{variable}} &= \bigcup_{i=0}^{n-1} {\big\{\{u, v\} \mid (u, v) \in S_{\lnot x_i}\times S_{x_i}\big\}}, \\ E_{\text{clause}} &= \bigcup_{j=0}^{m-1} {\big\{\{(j, 0), (j, 1)\}, \{(j, 1), (j, 2)\}, \{(j, 2), (j, 0)\}\big\}}, \\ E &= E_{\text{variable}} \cup E_{\text{clause}} \end{aligned} $$ と定義し、グラフ $G = (V, E)$ を考える。$|V| = 3m$ かつ $|E| \le nm^2+3m$ であるため、それぞれ $n+m$ の多項式で押さえられる。

このとき、$\phi$ が充足可能であることと $G$ がサイズ $m$ の独立集合を持つことが同値となる。

($\implies$): $\phi(\bm x) = 1$ なる $\bm x = (x_0, \dots, x_{n-1})$ が存在するとき、$G$ がサイズ $m$ の独立集合 $S$ を持つことを示す。

各節を充足するリテラル全体からなる集合を考える。すなわち、各 $j\in\Lambda_m$ に対して、 $$ T_j = \{k \in \Lambda_3 \mid x_{l_{j, k}} = a_{j, k}\} $$ で定義する。$\phi(\bm x) = 1$ から、各 $j$ に対して $T_j \ne \emptyset$ である。 $$ S = \{(j, \min T_j) \mid j\in\Lambda_m\} $$ とすると、$|S| = m$ が成り立つ。

任意の $i\in\Lambda_n$ に対して、$x_i = 0$ かつ $x_i = 1$ となることはないため、$E_{\text{variable}}$ に属する辺で結ばれた頂点同士が選ばれることはない。また、$S$ の構成から、$(j, k)\in S$ なる $j$ は相異なるため、$E_{\text{clause}}$ に属する辺で結ばれた頂点同士が選ばれることもない。よって、$S$ は $G$ における独立集合となっている。

($\impliedby$): $G$ がサイズ $m$ の独立集合 $S$ を持つとき、$\phi(\bm x) = 1$ なる $\bm x$ が存在することを示す。

各 $i\in\Lambda_n$ に対し、ある $j$, $k$ が存在して $l_{j, k} = i$ かつ $(j, k) \in S$ が成り立つとき $x_i = a_{j, k}$ とし、そうでないとき（どちらでもいいので適当に）$x_i = 0$ とする。 $E_{\text{variable}}$ に属する辺より、$(j, k), (j', k')$ が $(l_{j, k}, a_{j, k}) = (i, 0)$ かつ $(l_{j', k'}, a_{j', k'}) = (i, 1)$ を満たすとき $(j, k)\notin S$ または $(j', k')\notin S$ が成り立つ。すなわち、$x_i = 0$ かつ $x_i = 1$ となることはない。

また、各 $j\in\Lambda_m$ に対して、ある $k$ が存在して $(j, k)\in S$ かつ $l_{j, k}\in\Lambda_n$ が成り立つため、各 $j$ に対して $( (x_{l_{j, 0}} \harr a_{j, 0})\vee(x_{l_{j, 1}} \harr a_{j, 1})\vee(x_{l_{j, 2}} \harr a_{j, 2}) ) = 1$ が成り立つ。よって、$\phi(\bm x)=1$ となる。$\qed$

例

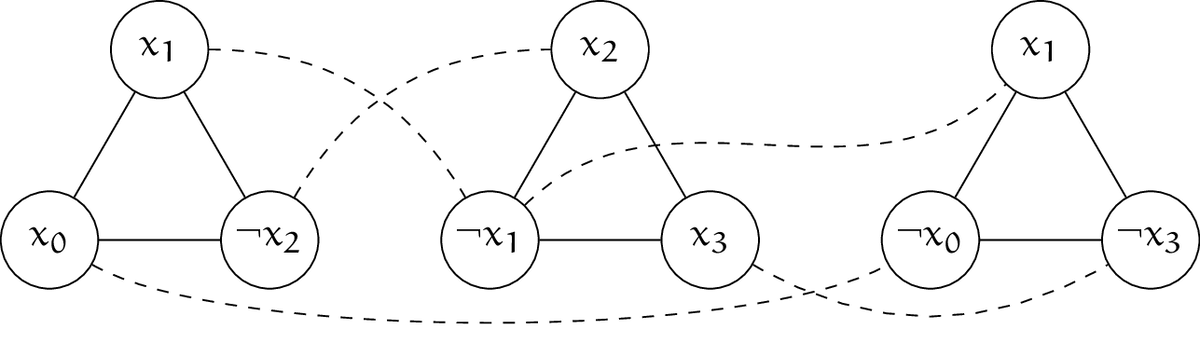
3-SAT の問題例 $\phi = (x_0\vee x_1\vee\lnot x_2)\wedge(\lnot x_1\vee x_2\vee x_3)\wedge(\lnot x_0\vee x_1\vee\lnot x_3)$ を考えます。変数は $n=4$ 個、節は $m=3$ 個です。 Claim 5 に示した方法に従って次のようにグラフ $G$ を構成します。

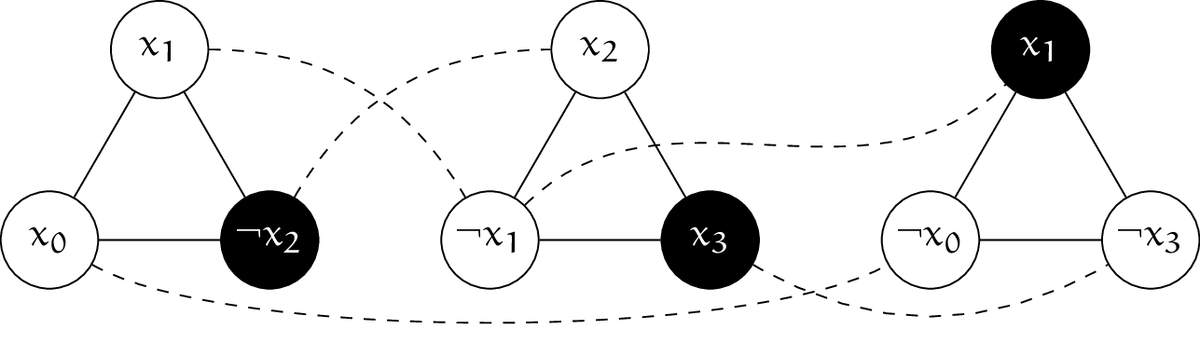
実線が $E_{\text{clause}}$、破線が $E_{\text{variable}}$ の辺を表しています。ただし、頂点のラベルは $(i, j)$ ではなく $i$ 番目の節の $j$ 個目のリテラルを書いています。このグラフ $G$ を用いて、Independent Set の問題例 $\theta = (G, 3)$ に帰着できます。

黒く塗った頂点 $\{(0, 2), (1, 2), (2, 1)\}$ が $\theta$ の certificate となるため、元の問題例においては $\lnot x_2 = x_3 = x_1 = 1$ とすればよいです。すなわち、$\bm x = (0, 1, 0, 1)$ が $\phi$ の certificate となります。$\eod$

3-Coloring

無向グラフ $G = (V, E)$ が与えられます。$3$-彩色関数 $c_3\colon V\to\Lambda_3$ を定められるか？という問題です。ただし、$\{u, v\}\in E$ ならば $c_3(u)\ne c_3(v)$ となる必要があります。 $c_3$ を定められるとき、$G$ は $3$-彩色可能である (is $3$-colorable) と言います。

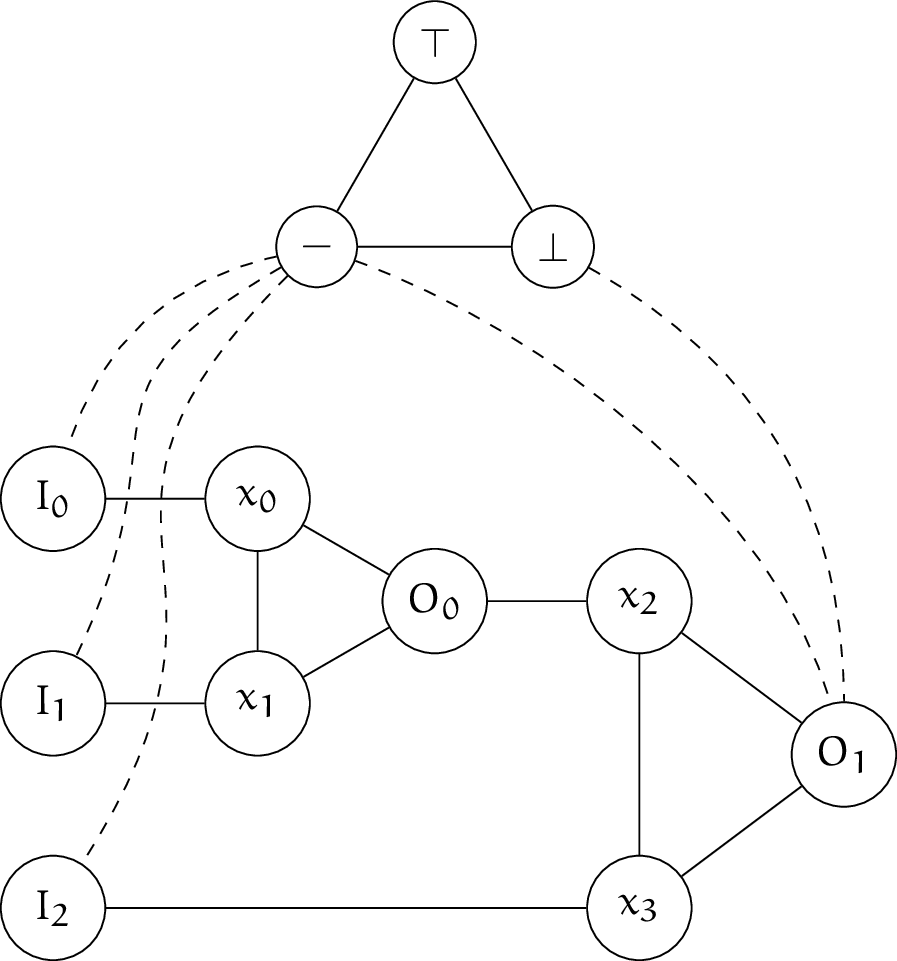
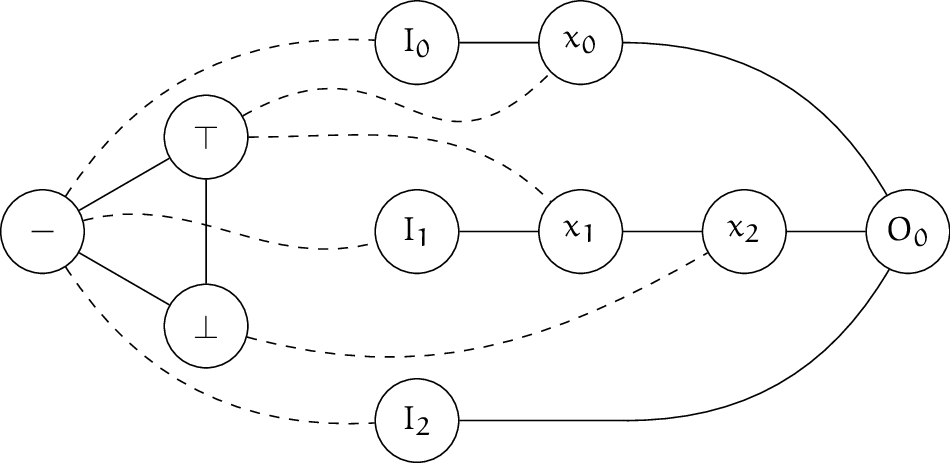
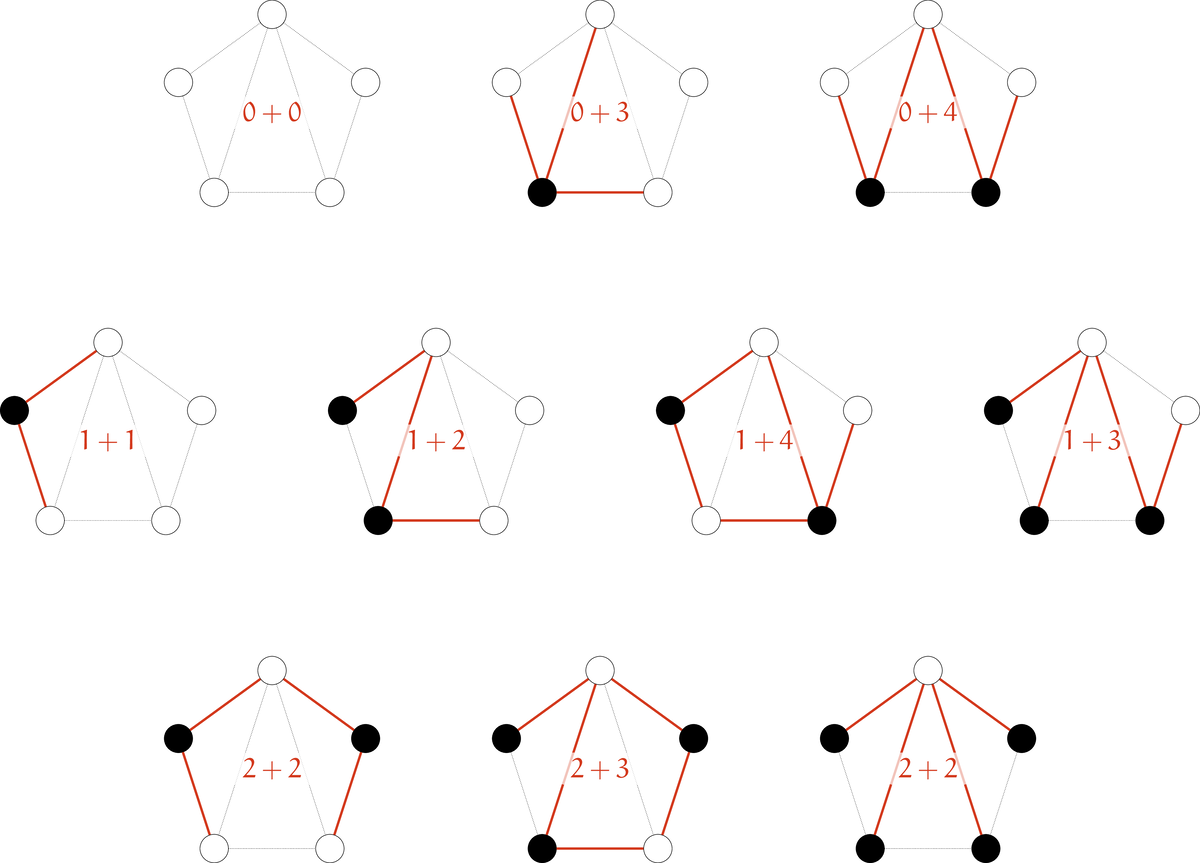
Lemma 6: 次のグラフに対する $3$-彩色を考える。

任意の $3$-彩色関数 $c$ について、$c(\top) \in \{c(I_0), c(I_1), c(I_2)\}$ かつ $c(O_1) = c(\top)$ が成り立つ。また、任意の $S \in 2^{\{I_0, I_1, I_2\}}\smallsetminus\{\emptyset\}$ に対し、ある $3$-彩色関数 $c$ が存在して $$ \{x\in\{I_0, I_1, I_2\}\mid c(x) = c(\top)\} = S $$ が成り立つ。

note: 見た目の都合で $-$ や $\bot$ と接続する辺を破線で描きましたが、実線で描いた他の辺と性質の差異があることを示唆するものではありません。

Proof

To-be-proved 1: 任意の $3$-彩色関数 $c$ に対して $c(O_1) = c(\top)$ が成り立つ。

$c(O_1) \ne c(-)$ かつ $c(O_1) \ne c(\bot)$ より $c(O_1) = c(\top)$ は明らか。

To-be-proved 2: 任意の $3$-彩色関数 $c$ に対して $c(\top) \in \{c(I_0), c(I_1), c(I_2)\}$ が成り立つ。

各 $i\in\Lambda_3$ に対して辺 $\{I_i, -\}$ が存在するため、$c(I_0) = c(I_1) = c(I_2) = c(\bot)$ なる $c$ を仮定して矛盾を導けばよい。

$c(x_0) \ne c(x_1)$ に注意すると、$c(I_0) = c(I_1)$ ならば $c(O_0) = c(I_0)$ が成り立つことがわかる。同様にして、$c(O_0) = c(I_2)$ ならば $c(O_1) = c(O_0)$ となる。

以上より、$c(I_0) = c(I_1) = c(I_2) = c(\bot)$ ならば $c(O_1) = c(\bot)$ となるが、$c(O_1) = c(\top)$ に矛盾する。よって、$c(\top) \in \{c(I_0), c(I_1), c(I_2)\}$ が従う。

To-be-proved 3: 任意の $S \in 2^{\{I_0, I_1, I_2\}}\smallsetminus\{\emptyset\}$ に対し、$\{x\in\{I_0, I_1, I_2\}\mid c(x) = c(\top)\} = S$ なる $3$-彩色関数 $c$ が存在する。

次のようにして構成できる。以下では、$I_0$ などを論理変数として扱い、$c(I_0) = c(\top)$ とすることを $I_0 = \top$ のように表記する。

$O_0 = I_0\vee I_1$ とする。
$I_0 = I_1$ のとき、$(x_0, x_1) = (\lnot I_0, -)$ とする。
$I_0 \ne I_1$ のとき、$I_i = \top$ なる $i\in\{0, 1\}$ に対して $x_i = \bot$ とし、$x_{1-i} = -$ とする。
$(O_0, I_2, x_2, x_3, O_1)$ を $(I_0, I_1, x_0, x_1, O_0)$ と見なして上記の手続きを行う。

以上の手続きによる割り当ての表は次のようになる。

$I_0$	$I_1$	$x_0$	$x_1$	$O_0$
$\bot$	$\bot$	$\top$	$-$	$\bot$
$\bot$	$\top$	$-$	$\bot$	$\top$
$\top$	$\bot$	$\bot$	$-$	$\top$
$\top$	$\top$	$\bot$	$-$	$\top$

$I_0$	$I_1$	$I_2$	$x_0$	$x_1$	$O_0$	$x_2$	$x_3$	$O_1$
$\bot$	$\bot$	$\top$	$\top$	$-$	$\bot$	$-$	$\bot$	$\top$
$\bot$	$\top$	$\bot$	$-$	$\bot$	$\top$	$\bot$	$-$	$\top$
$\bot$	$\top$	$\top$	$-$	$\bot$	$\top$	$\bot$	$-$	$\top$
$\top$	$\bot$	$\bot$	$\bot$	$-$	$\top$	$\bot$	$-$	$\top$
$\top$	$\bot$	$\top$	$\bot$	$-$	$\top$	$\bot$	$-$	$\top$
$\top$	$\top$	$\bot$	$\bot$	$-$	$\top$	$\bot$	$-$	$\top$
$\top$	$\top$	$\top$	$\bot$	$-$	$\top$	$\bot$	$-$	$\top$

以上で示された。$\qed$

$\{O_1, \bot\}$ の辺を除いたグラフにおいて $O_1 = I_0\vee I_1\vee I_2$ なる $3$-彩色が可能であることや、$I_0=I_1=I_2=\bot$ のとき $O_1=\bot$ なる $3$-彩色しかできないことを利用しています*10。

このグラフを利用して 3-SAT から 3-Coloring への帰着を行います。上記のグラフのように、帰着の際に補助的に使う部品は、しばしば gadget と呼ばれます。「何々 gadget」の何々の部分は各文脈での著者のお気持ち命名で、固有名詞的な使われ方はしていないと思います。

Claim 7: 3-Coloring は 3-SAT から帰着できる。

Proof

sketch: Lemma 6 で示した OR-gate gadget を各節について構成する。

3-SAT の問題例を $$ \phi = \bigwedge_{i=0}^{m-1} {(\alpha_{i, 0}\vee\alpha_{i, 1}\vee\alpha_{i, 2})} $$ とし、変数の個数を $n$ とする。すなわち、$x_0, \dots, x_{n-1}$ であるとする。

OR-gate gadget $\gamma$ を次で定義する。 $$ \begin{aligned} &\phantom{{}={}} \gamma(\alpha_0, \alpha_1, \alpha_2, y_0, y_1, y_2, y_3, y_4, y_5) \\ &= \{ \{\alpha_0, y_0\}, \{\alpha_1, y_1\}, \{y_0, y_1\}, \{y_1, y_2\}, \\ &\qquad\qquad \{y_2, y_0\}, \{y_2, y_3\}, \{\alpha_2, y_4\}, \{y_3, y_4\}, \\ &\qquad\qquad \{y_4, y_5\}, \{y_5, y_3\}, \{y_5, -\}, \{y_5, \bot\} \}. \end{aligned} $$ note: Lemma 6 の図は $\gamma(I_0, I_1, I_2, x_0, x_1, O_0, x_2, x_3, O_1)$ に相当する。

帰着させるグラフのための変数を次のように定義する。 $$ \begin{aligned} V_{\text{positive}} &= \{x_0, \dots, x_{n-1}\}, \\ V_{\text{negative}} &= \{\lnot v\mid v\in V_{\text{positive}}\}, \\ V_{\text{const}} &= \{\top, \bot, -\}, \\ V_{\text{clause}} &= \{y_{i, j} \mid (i, j) \in \Lambda_m \times \Lambda_5\}, \\ E_{\text{logic}} &= \{\{v, \lnot v\}\mid v\in V_{\text{positive}}\} \cup \{\{v, -\} \mid v\in V_{\text{positive}} \cup V_{\text{negative}}\} \\ & \qquad\quad {} \cup \{\{\top, \bot\}, \{\top, -\}, \{\bot, -\}\}, \\ E_{\text{clause}} &= \bigcup_{i=0}^{m-1} \gamma(\alpha_{i, 0}, \alpha_{i, 1}, \alpha_{i, 2}, y_{i, 0}, y_{i, 1}, y_{i, 2}, y_{i, 3}, y_{i, 4}, y_{i, 5}). \end{aligned} $$ 上記を用いて、 $$ \begin{aligned} V &= V_{\text{positive}} \cup V_{\text{negative}} \cup V_{\text{const}} \cup V_{\text{clause}}, \\ E &= E_{\text{logic}} \cup E_{\text{clause}} \end{aligned} $$ で定義する。$\theta = (V, E)$ が $\phi$ に対応する 3-Coloring の問題例となる。

$E_{\text{logic}}$ により、各 $i$ について $c(x_i)\ne c(\lnot x_i)$ かつ $\{c(x_i), c(\lnot x_i)\} = \{c(\top), c(\bot)\}$ となることに注意せよ。

($\implies$): $\phi$ が充足可能なとき、$\theta$ が $3$- 彩色可能であることを示す。

$\phi$ が充足可能なとき、$x_i = 1$ なる各 $i$ について $c(x_i) = c(\top)$ かつ $c(\lnot x_i) = c(\bot)$ とする。また、$x_i = 0$ なる各 $i$ について $c(x_i) = c(\bot)$ かつ $c(\lnot x_i) = c(\top)$ とする。$\phi$ の充足可能性より、$V_{\text{clause}}$ の各頂点に対しては、Lemma 6 で示したようにして彩色できる。

($\impliedby$): $\theta$ が $3$-彩色可能なとき、$\phi$ が充足可能であることを示す。

各 $i$ に対して $c(y_{i, 5}) = c(\top)$ であり、Lemma 6 より $c(\top)\in\{c(\alpha_{i, 0}), c(\alpha_{i, 1}), c(\alpha_{i, 2})\}$ である。また、各 $i$ に対して $c(x_i)\ne c(\lnot x_i)$ である。

よって、$c(x_i) = c(\top)$ なる $x_i$ に対して $x_i = 1$、$c(x_i) = c(\bot)$ なる $x_i$ に対して $x_i = 0$ と割り当てることで、$\phi$ を充足することができる。

以上より、変数 $n$ 個、節 $m$ 個の 3-SAT を、頂点 $2n+6m+3$ 個、辺 $3n+12m+3$ 本のグラフにおける $3$-彩色問題に帰着できた。$\qed$

Lemma 8: 次のグラフにおける $3$-彩色 $c$ を考える。

このグラフが $3$-彩色可能であることは、$c(\top)\in\{c(I_0), c(I_1), c(I_2)\}$ と同値である。

Rationale

証明は場合分けなどにより容易であるから、背景を述べる。

入力 $I_0$, $I_1$, $I_2$ を定めると、$O_0$ に隣接する頂点 $x_0$, $x_2$, $I_2$ の選択肢の集合がそれぞれ独立に定まる。

入力の条件	出力変数	$\top$	$\bot$	$-$
$c(I_0) = c(\bot)$	$x_0$			○
$c(I_0) = c(\top)$	$x_0$		○	○
$c(I_1) = c(\bot)$	$x_2$	○
$c(I_1) = c(\top)$	$x_2$	○		○
$c(I_2) = c(\bot)$	$I_2$		○
$c(I_2) = c(\top)$	$I_2$	○

$c(I_0) = c(I_1) = c(I_2) = c(\bot)$ のときは選択肢の集合が互いに素であるため $c(O_0)$ を定めることができない。一方、$c(I_i) = c(\top)$ なる $i\in\Lambda_3$ が存在したとき、選択肢に重複が生じるため、残った色を $O_0$ に割り当てることで彩色が可能となる。$\qed$

Lemma 8 の gadget を用いて帰着することももちろんできます。こちらは頂点 $2n+4m+3$ 個、辺 $3n+9m+3$ 本となります。 Lemma 6 の gadget と異なり、$O_0$ の色はなんでもよいことに注意しましょう。

例

3-SAT の問題例 $\phi = (x_0\vee x_1\vee\lnot x_2)\wedge(\lnot x_1\vee x_2\vee x_3)\wedge(\lnot x_0\vee x_1\vee\lnot x_3)$ を考えます。変数は $n=4$ 個、節は $m=3$ 個です。Independent Set の章で用いたものと同様の例です。

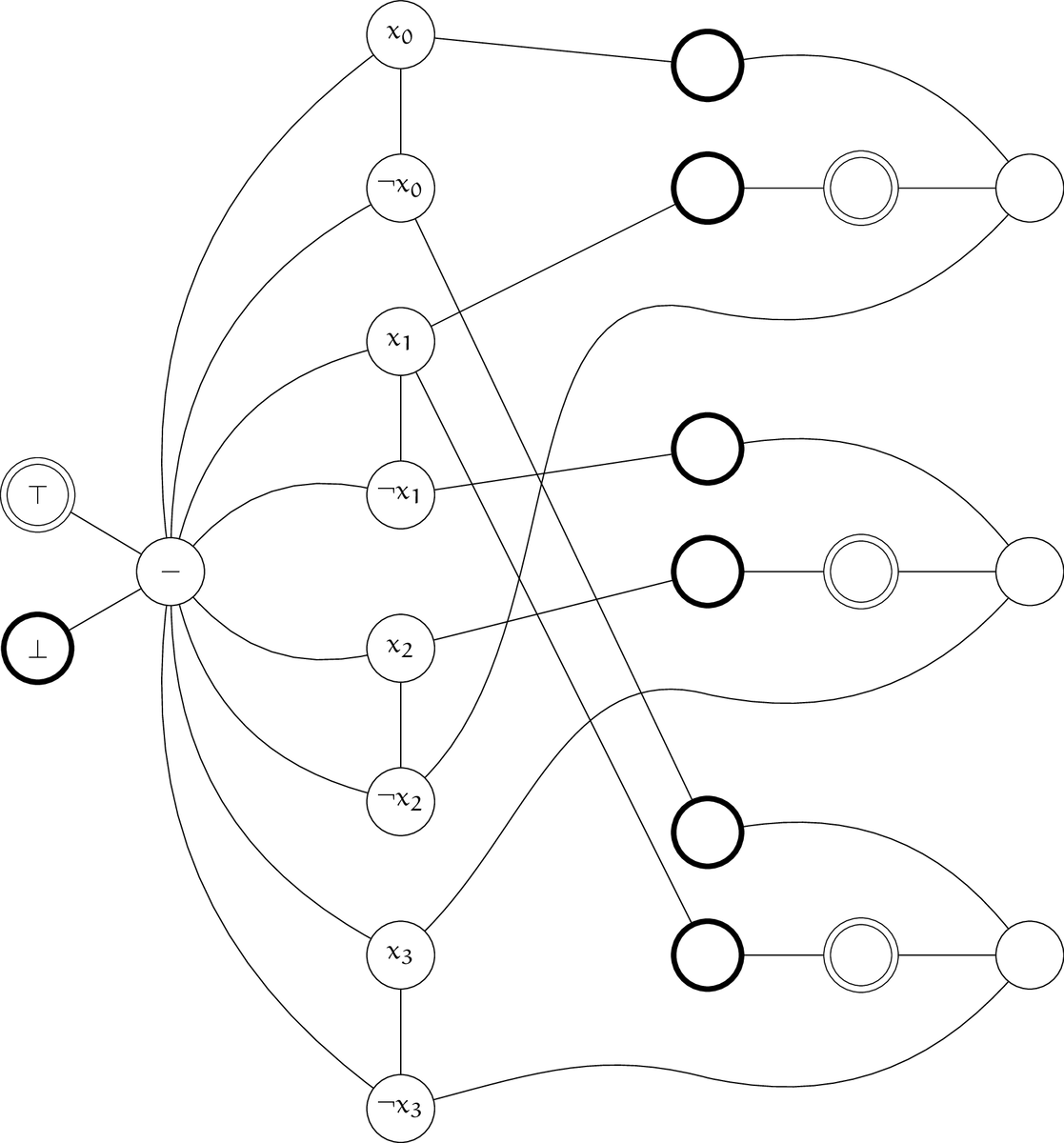
Lemma 8 の gadget を用いて帰着します。gadget の部分以外は Claim 7 で示した通りです。作図の都合上、太線で囲んだ頂点は $\top$ の頂点と辺で結ばれていることを意味するものとします。同様に、二重線で囲んだ頂点は $\bot$ の頂点と結ばれているとします。

次に示すグラフが、対応する 3-Coloring の問題例 $\theta$ となります。真ん中の列が Lemma 8 で言うところの $I_0$, $I_1$, $I_2$ に対応し、右側の列が $x_0$, $x_1$, $x_2$, $O_0$ に相当します。

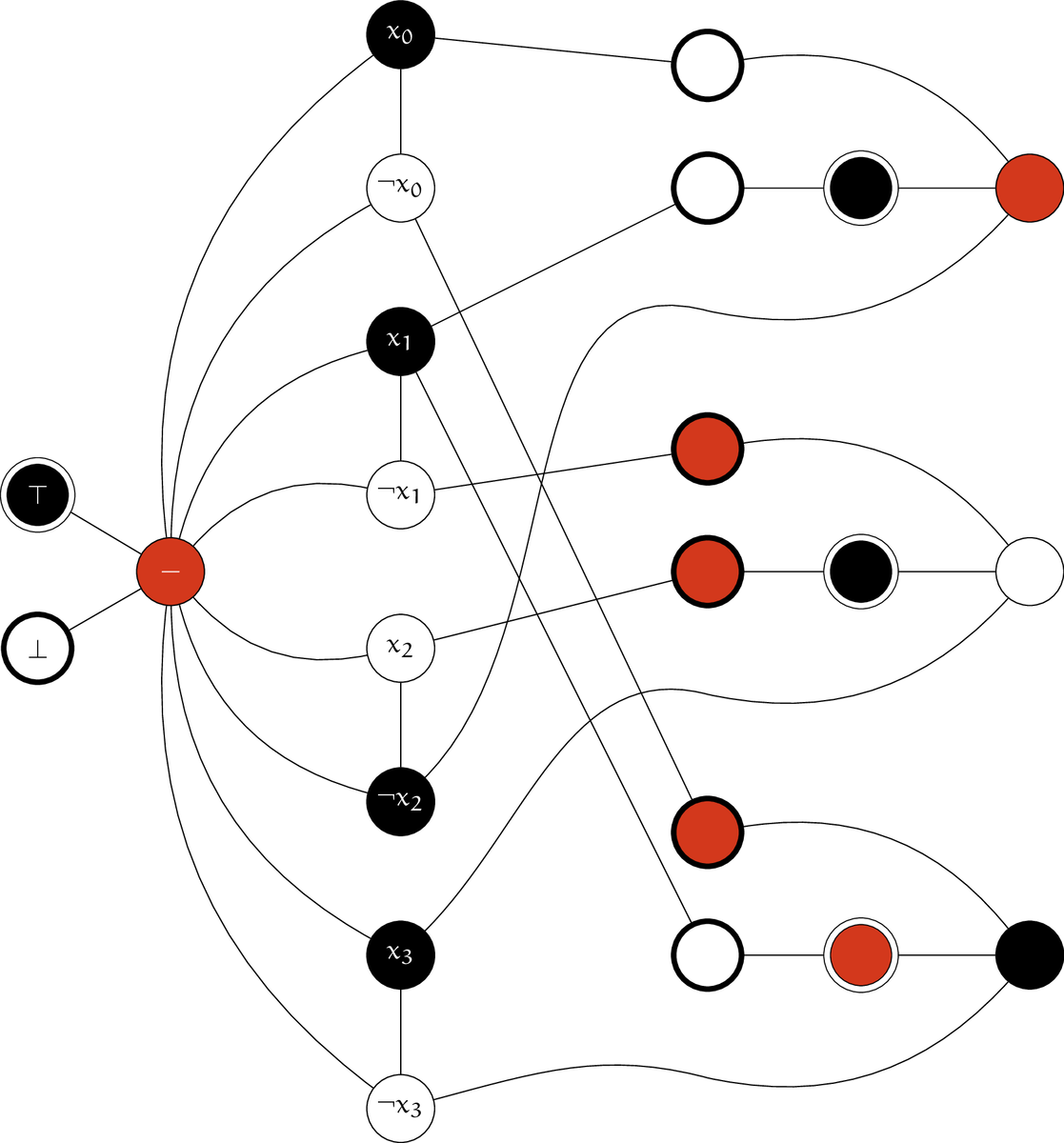
これを解いて、次の certificate を得ます。

よって、$\phi$ に対する certificate として $\bm x = (1, 1, 0, 1)$ を得ます*11。$\eod$

3-Dimensional Matching (3DM)

3 つの有限集合 $X$, $Y$, $Z$ と集合 $T\subseteq X\times Y\times Z$ が与えられます。ここで、$|X|=|Y|=|Z|$ です。これに対し、完全マッチング (perfect matching) が存在するか？という問題です。

集合 $M\subseteq T$ が $(X\times Y\times Z, T)$ の完全マッチングであるとは、以下の条件をすべて満たすことを指します。

$|M| = |X|$,
$\{x\mid (x, y, z)\in M\} = X$,
$\{y\mid (x, y, z)\in M\} = Y$, and
$\{z\mid (x, y, z)\in M\} = Z$.

次のように言うこともできます。

相異なる $(x, y, z), (x', y', z')\in M$ について、$x\ne x'$ かつ $y\ne y'$ かつ $z\ne z'$ が成り立つ。
任意の $x\in X$ について、ある $y\in Y$, $z\in Z$ が存在して $(x, y, z) \in M$ が成り立つ。
任意の $y\in Y$ について、ある $x\in X$, $z\in Z$ が存在して $(x, y, z) \in M$ が成り立つ。
任意の $z\in Z$ について、ある $x\in X$, $y\in Y$ が存在して $(x, y, z) \in M$ が成り立つ。

例

$$ \begin{aligned} X &= \{x_0, x_1, x_2, x_3\}, \\ Y &= \{y_0, y_1, y_2, y_3\}, \\ Z &= \{z_0, z_1, z_2, z_3\}, \\ T &= \{(x_0, y_1, z_3), (x_1, y_0, z_2), (x_1, y_2, z_3), (x_2, y_3, z_0), (x_3, y_2, z_1)\} \end{aligned} $$ に対し、$\phi = ( (X, Y, Z), T)$ です。

$S = \{(x_0, y_1, z_3), (x_1, y_0, z_2), (x_2, y_3, z_0), (x_3, y_2, z_1)\}$ は条件を満たします。$\eod$

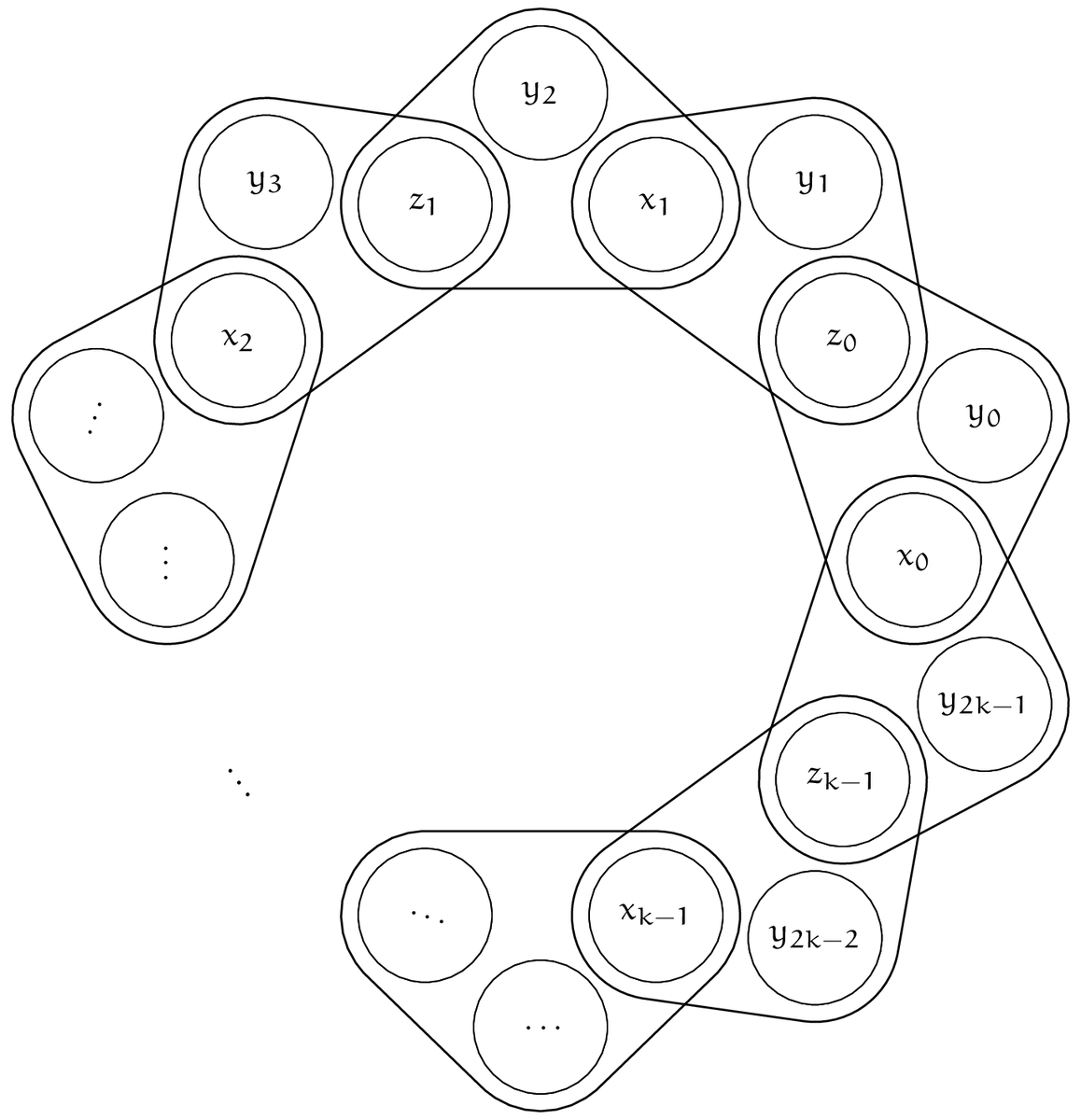
Lemma 9: 集合 $X$, $Y$, $Z$, $T$ に対し、 $$ \begin{aligned} X' &= \{x_0, \dots, x_{k-1}\} \subseteq X, \\ Y' &= \{y_0, \dots, y_{2k-1}\} \subseteq Y, \\ Z' &= \{z_0, \dots, z_{k-1}\} \subseteq Z, \\ T_{\text{even}}' &= \{(x_i, y_{2i}, z_i) \mid 0\le i\lt k\} \subseteq T, \\ T_{\text{odd}}' &= \{(x_{(i+1)\bmod k}, y_{2i+1}, z_i)\mid 0\le i\lt k\} \subseteq T, \\ T' &= T_{\text{even}}' \cup T_{\text{odd}}' \end{aligned} $$ なる $X'$, $Y'$, $Z'$, $T'$ が存在したとする（下図も参考にせよ）。

さらに、$X'$ および $Z'$ の元を含む組は $T\smallsetminus T'$ には存在しないとする。すなわち、 $$ \begin{aligned} % \{(x, y, z)\in T\mid x = x_i\} &= \{(x_i, y_{2i}, z_i), (x_i, y_{(2i-1)\bmod k}, z_{(i-1)\bmod k})\}, \\ % \{(x, y, z)\in T\mid z = z_i\} &= \{(x_i, y_{2i}, z_i),(x_{(i+1)\bmod k}, y_{2i+1}, z_i)\} \{(x, y, z)\in T \mid x\in X' \vee z\in Z'\} &= T' \end{aligned} $$ が成り立つとする。このとき、$(X\times Y\times Z, T)$ の任意の完全マッチング $M$ は、 $(M\supseteq T_{\text{even}}')\wedge(M\cap T_{\text{odd}}' = \emptyset)$ または $(M\supseteq T_{\text{odd}}')\wedge(M\cap T_{\text{even}}' = \emptyset)$ を満たす。

Proof

$\{(x, y, z)\in T\mid z = z_0\} = \{(x_0, y_0, z_0), (x_1, y_1, z_0)\}$ であるから、$(x_0, y_0, z_0) \in M$ または $(x_1, y_1, z_0) \in M$ が成り立つ。

Case 1: $(x_0, y_0, z_0) \in M$

$(x_0, y_0, z_0) \in T_{\text{even}}'$ であるから、$(M\supseteq T_{\text{even}}')\wedge(M\cap T_{\text{odd}}' = \emptyset)$ を示す。

$$ \begin{aligned} P(i) &\iff (x_{i\bmod k}, y_{2i\bmod k}, z_{i\bmod k}) \in M, \\ Q(i) &\iff (x_{(i+1)\bmod k}, y_{(2i+1)\bmod k}, z_{i\bmod k}) \notin M \end{aligned} $$ とし、$i$ について帰納的に示す。$P(i)\implies Q(i)$ と $Q(i)\implies P(i+1)$ を示す。

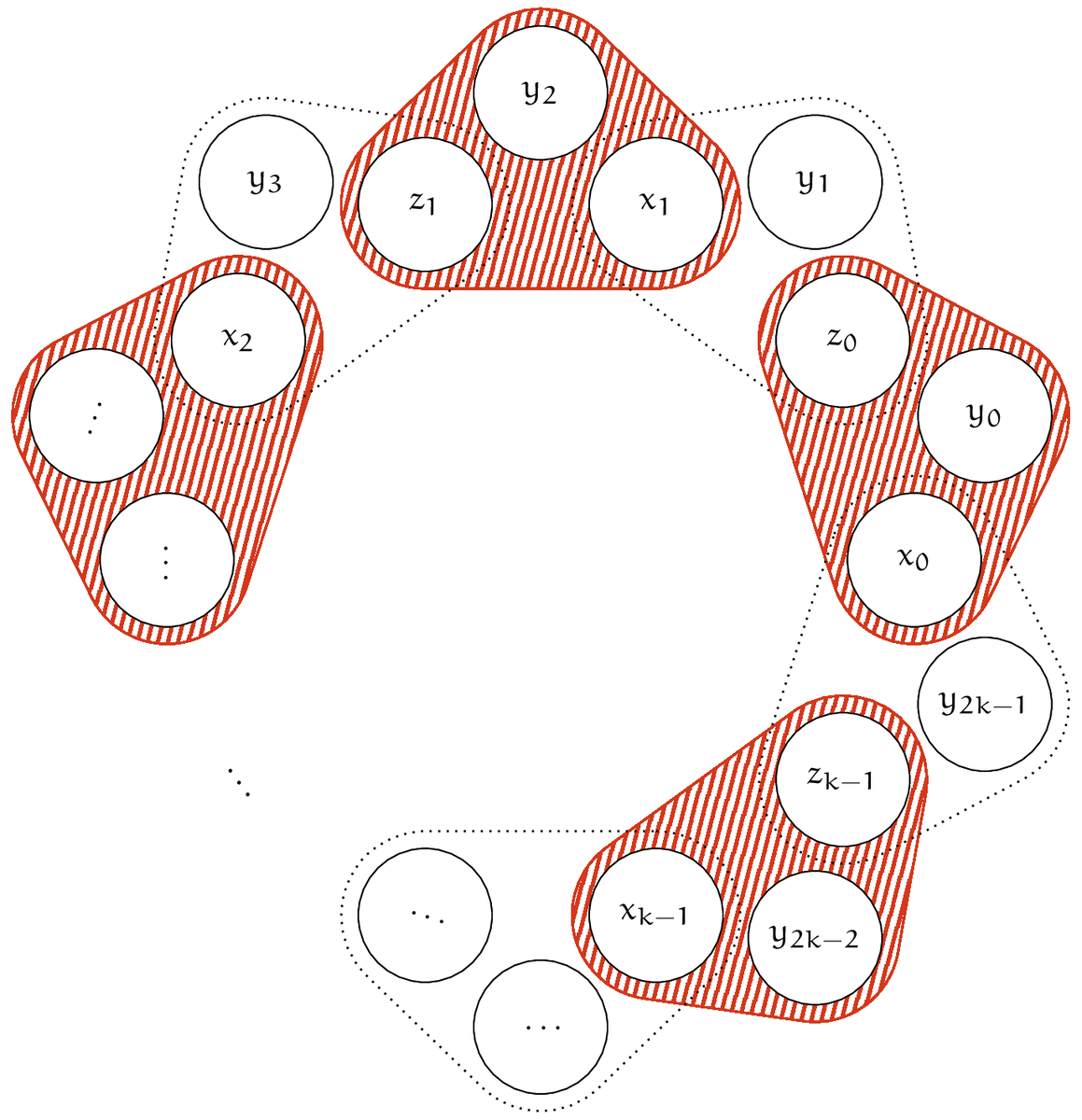
To-be-proved 1: $P(i)\implies Q(i)$

$(x_{i\bmod k}, y_{2i\bmod k}, z_{i\bmod k}) \in M$ であるから、$z_{i\bmod k}$ に着目すると $(x_{(i+1)\bmod k}, y_{(2i+1)\bmod k}, z_{i\bmod k}) \notin M$ が従う。

To-be-proved 2: $Q(i)\implies P(i+1)$

$$ P(i+1) \iff (x_{(i+1)\bmod k}, y_{2(i+1)\bmod k}, z_{(i+1)\bmod k}) \in M $$ である。$(x_{(i+1)\bmod k}, y_{(2i+1)\bmod k}, z_{i\bmod k}) \notin M$ であるから、$\lnot P(i+1)$ とすると $(x_{(i+1)\bmod k}, y, z)\in M$ なる $(y, z)\in Y\times Z$ が存在せず、完全マッチングの条件に反する。よって、$Q(i)\implies P(i+1)$ が成り立つ。

以上より、$(x_0, y_0, z_0) \in M$ ならば $(M\supseteq T_{\text{even}}')\wedge(M\cap T_{\text{odd}}' = \emptyset)$ が成り立つ。

Case 2: $(x_1, y_1, z_0) \in M$

対称性より、Case 1 と同様にして $(M\supseteq T_{\text{odd}}')\wedge(M\cap T_{\text{even}}' = \emptyset)$ が示せる。$\qed$

note: $y$ の添字が偶数のものを一つでも選んだら $y$ の添字が偶数のもの全体を選ぶのを強制され、奇数の方は選べません。偶奇が逆の場合も同様です。これを、3-SAT の各変数 $x_i$ が複数の節に現れる際の $0$ や $1$ への割り当ての一貫性の担保のために使います。

Claim 10: 3DM は 3-SAT から帰着できる。

Proof

3-SAT の問題例を $$ \phi = \bigwedge_{j=0}^{m-1} ( (x_{l_{j, 0}}\harr a_{j, 0}) \vee (x_{l_{j, 1}}\harr a_{j, 1}) \vee (x_{l_{j, 2}}\harr a_{j, 2}) ) $$ とし、$n$ 個の変数を $x_0, \dots, x_{n-1}$ とする。

各 $i\in\Lambda_n$ に対して変数 $x_i$ が節に出現する回数を $c_i$ とする。すなわち、 $$ c_i = |{\{(j, k) \in \Lambda_m\times\Lambda_3 \mid l_{j, k} = i\}}| $$ である。ここで、$l_{j, k}\in \Lambda_m$ より $$ \sum_{i=0}^{n-1} c_i = |{\Lambda_m\times\Lambda_3}| = 3m $$ が成り立つことに注意せよ。さて、 $$ \begin{aligned} X_{\text{variable}} &= \bigcup_{i=0}^{n-1} {\{u_{i, 0}, \dots, u_{i, c_i-1}\}}, \\ X_{\text{clause}} &= \bigcup_{j=0}^{m-1} {\{v_{j, 0}, v_{j, 1}, v_{j, 2}\}}, \\ Y_{\text{literal}} &= \bigcup_{i=0}^{n-1} {\{w_{i, 0, 0}, w_{i, 0, 1}, \dots, w_{i, c_i-1, 0}, w_{i, c_i-1, 1}\}}, \\ Z_{\text{variable}} &= \bigcup_{i=0}^{n-1} {\{u_{i, 0}', \dots, u_{i, c_i-1}'\}}, \\ Z_{\text{clause}} &= \bigcup_{j=0}^{m-1} {\{v_{j, 0}', v_{j, 1}', v_{j, 2}'\}} \end{aligned} $$ で定義する。これを用いて $$ \begin{aligned} X &= X_{\text{variable}} \cup X_{\text{clause}}, \\ Y &= Y_{\text{literal}}, \\ Z &= Z_{\text{variable}} \cup Z_{\text{clause}} \end{aligned} $$ とする。このとき $$ \begin{aligned} |X| &= |X_{\text{variable}}| + |X_{\text{clause}}| \\ &= \sum_{i=0}^{n-1} c_i + 3m = 6m, \\ |Y| &= |Y_{\text{literal}}| \\ &= \sum_{i=0}^{n-1} 2c_i = 6m, \\ |Z| &= |X| = 6m \end{aligned} $$ より、$|X|=|Y|=|Z|$ が成り立つ。

さて、Lemma 9 を踏まえ、consistency gadget $\gamma_{\text{variable}}$ を次のように定義する。 $$ \begin{aligned} \gamma_{\text{discard-false}}(i) &= \{(u_{i, j}, w_{i, j, 0}, u_{i, j}') \mid j\in\Lambda_{c_i}\}, \\ \gamma_{\text{discard-true}}(i) &= \{(u_{i, (j+1)\bmod c_i}, w_{i, j, 1}, u_{i, j}') \mid j\in\Lambda_{c_i}\} \\ \gamma_{\text{variable}}(i) &= \gamma_{\text{discard-false}}(i) \cup \gamma_{\text{discard-true}}(i). \end{aligned} $$ また、各節に対応する satisfaction gadget $\gamma_{\text{clause}}$ を次のように定義する。

各 $(j, k)$ に対し、変数 $x_{l_{j, k}}$ が何番目の出現かを考える。すなわち $$ \nu_{j, k} = |{\{(j', k')\in\Lambda_m\times\Lambda_3 \mid l_{j', k'} = l_{j, k} \wedge (j', k')\lt (j, k)\}}| $$ とする。ただし、$\lt$ は辞書順とする*12。また、簡便さのため $$ \begin{aligned} y_{j, k} &= w_{l_{j, k}, \nu_{j, k}, a_{j, k}}, & {\bar y}_{j, k} &= w_{l_{j, k}, \nu_{j, k}, \lnot a_{j, k}} \end{aligned} $$ とし、これを用いて、 $$ \begin{aligned} \gamma_{\text{clause}}(j) &= \{(v_{j, 0}, y, v_{j, 0}') \mid y\in\{y_{j, 0}, y_{j, 1}, y_{j, 2}\}\} \\ & \qquad\quad {} \cup \{(v_{j, 1}, y, v_{j, 1}') \mid y\in\{y_{j, 0}, \bar y_{j, 0}, y_{j, 1}, \bar y_{j, 1}, y_{j, 2}, \bar y_{j, 2}\}\} \\ & \qquad\quad {} \cup \{(v_{j, 2}, y, v_{j, 2}') \mid y\in\{y_{j, 0}, \bar y_{j, 0}, y_{j, 1}, \bar y_{j, 1}, y_{j, 2}, \bar y_{j, 2}\}\} \end{aligned} $$ とする。

$$ T = \left(\bigcup_{i=0}^{n-1} \gamma_{\text{variable}}(i)\right) \cup \left(\bigcup_{j=0}^{m-1} \gamma_{\text{clause}}(j)\right) $$ とする。このとき、$\theta = ( (X, Y, Z), T)$ に完全マッチングが存在することと、$\phi$ が充足可能であることは同値である。

($\implies$): $M$ が $\theta$ の完全マッチングであるとき、$\phi(\bm x) = 1$ なる $\bm x$ を構成できることを示す。

各 $i\in\Lambda_n$ に対して、$\gamma_{\text{discard-false}}(i) \subseteq M$ のとき $x_i = 1$、$\gamma_{\text{discard-true}}(i) \subseteq M$ のとき $x_i = 0$ とする。

各 $j\in\Lambda_m$ に対して $$ \{(x, y, z)\in T\mid x=v_{j, 0}\vee z=v_{j, 0}'\} = \{v_{j, 0}\}\times\{y_{j, 0}, y_{j, 1}, y_{j, 2}\}\times\{v_{j, 0}'\} $$ であり、ちょうど一つの $k\in\Lambda_3$ に対して $(v_{j, 0}, y_{j, k}, v_{j, 0}')\in M$ が成り立つ。また、Lemma 9 を踏まえると、ある $(u, u')\in X\times Z$ が存在して $(u, \bar y_{j, k}, u')\in M$ が成り立つことがわかる。以上より、$x_{l_{j, k}} = a_{j, k}$ が従うため、 $$( (x_{l_{j, 0}}\harr a_{j, 0})\wedge(x_{l_{j, 1}}\harr a_{j, 1})\wedge(x_{l_{j, 2}}\harr a_{j, 2}) ) = 1$$ が成り立つ。

($\impliedby$): $\bm x$ が $\phi(\bm x) = 1$ を満たすとき、$\theta$ の完全マッチング $M$ を構成できることを示す。

各 $i\in\Lambda_n$ に対して、$x_i = 0$ のとき、任意の $t\in\gamma_{\text{discard-true}}(i)$ に対して $t\in M$ とし、$x_i = 1$ のとき、任意の $t\in\gamma_{\text{discard-false}}(i)$ に対して $t\in M$ とする。

また、各 $j\in\Lambda_m$ に対し、ある $k\in\Lambda_3$ が存在して $x_{l_{j, k}} = a_{j, k}$ が成り立つから、その $k$ に対して $(v_{j, 0}, y_{j, k}, v_{j, 0}')\in M$ とする。

さらに、$\{k', k''\} = \Lambda_3\smallsetminus\{k\}$ とする。$x_{l_{j, k'}} = a_{j, k'}$ のとき $(v_{j, 1}, y_{j, k'}, v_{j, 1}')\in M$ とし、$x_{l_{j, k'}} \ne a_{j, k'}$ のとき $(v_{j, 1}, \bar y_{j, k'}, v_{j, 1}')\in M$ とする。$k''$ についても $v_{j, 2}$ と $v_{j, 2}'$ について同様にする。

上記以外の $t\in T$ については $t\notin M$ とする。これは完全マッチングの条件を満たしている。$\qed$

補足

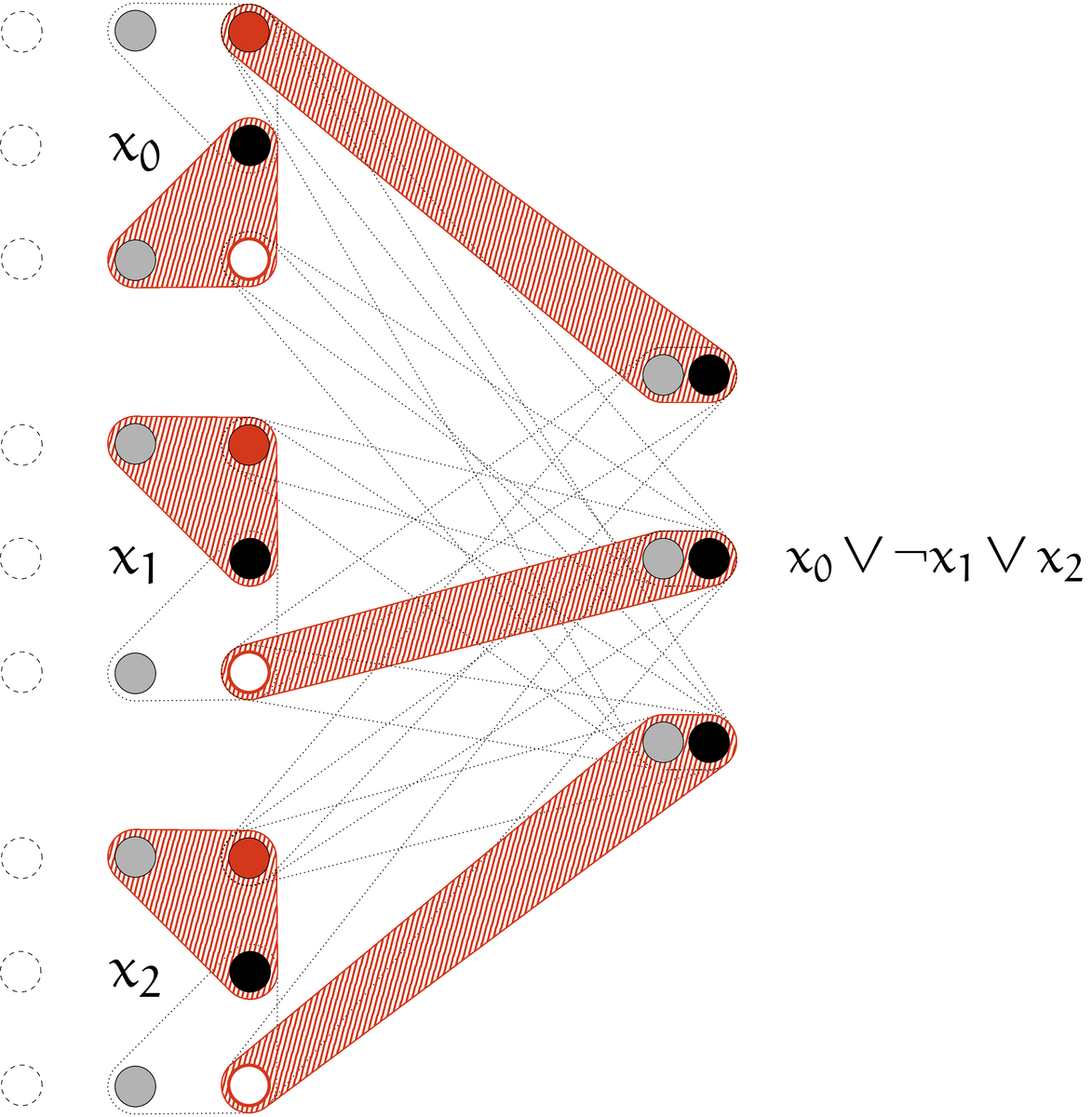
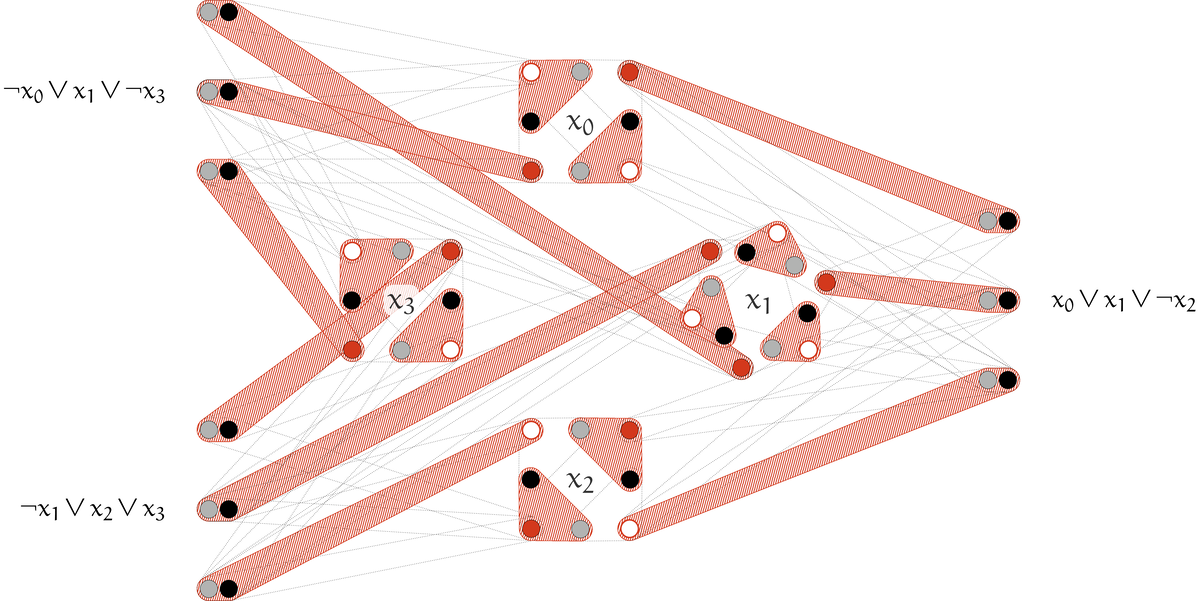
左半分が consistency gadget で、灰色の頂点が $u_{i, j}\in X$、黒色の頂点が $u_{i, j}'\in Z$、赤線白色の頂点が $w_{i, j, 0}\in Y$、赤色の頂点が $w_{i, j, 1}\in Y$ に対応します。右半分が satisfaction gadget で、灰色の頂点が $v_{i, j}\in X$、黒色の頂点が $v_{i, j}'\in Z$ に対応します。 satisfaction gadget のうち $v_{j, 0}\in X$ と $v_{j, 0}'\in Z$ を含む組は、その節を充足するリテラルのみを選択できるようにし、残りの組は任意のリテラルを選択できるようにしています。$\eod$

例

3-SAT の問題例 $\phi = (x_0\vee x_1\vee\lnot x_2)\wedge(\lnot x_1\vee x_2\vee x_3)\wedge(\lnot x_0\vee x_1\vee\lnot x_3)$ を考えます。変数は $n=4$ 個、節は $m=3$ 個です。以前の章で用いたものと同様の例です。

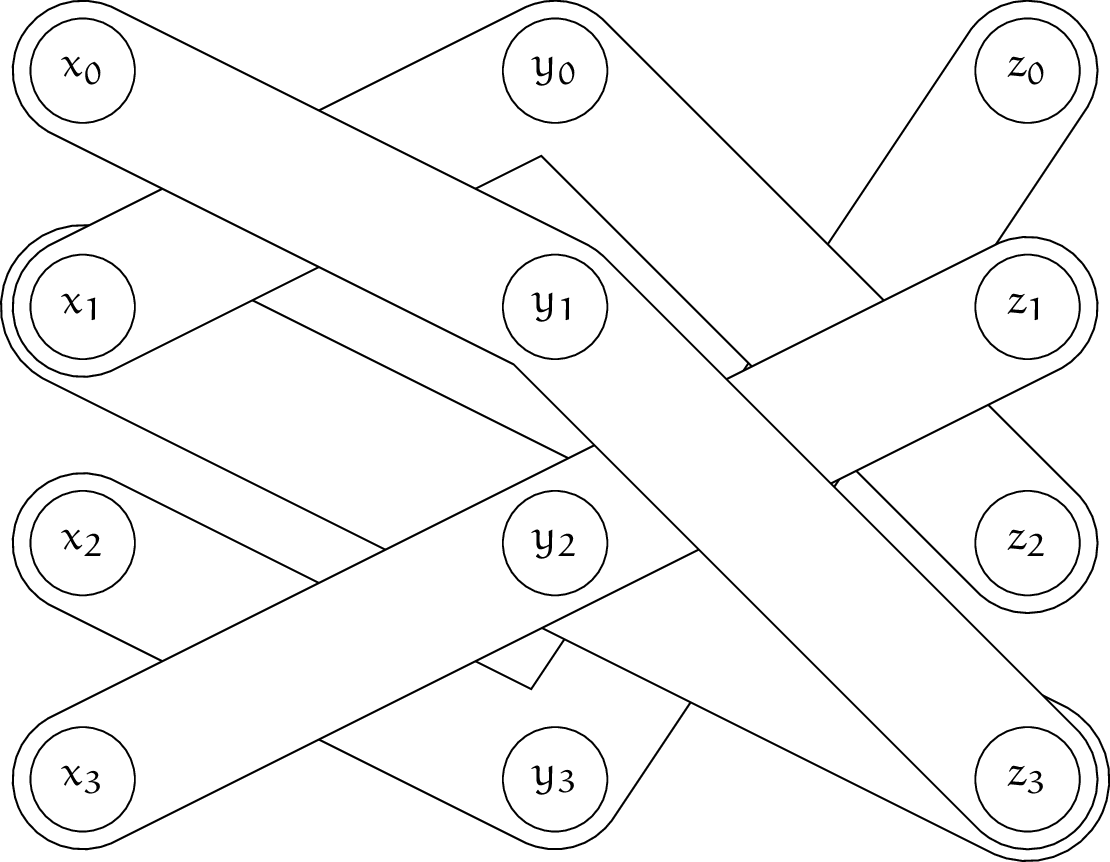
Claim 10 に従って構成した $\theta$ における certificate は下記の通りです。$3$ つ組があまりにも入り乱れているため、素の $\theta$ の図は割愛し、完全マッチングの certificate を明示した図のみを載せます。

マッチングのうち consistency gadget を含む部分から、$\bm x = (1, 1, 0, 1)$ が構成できます。satisfaction gadget を含む部分から、$x_0\vee x_1\vee\lnot x_2$ は $x_0$ が、$\lnot x_1\vee x_2\vee x_3$ は $x_3$ が、$\lnot x_0\vee x_1\vee\lnot x_3$ は $x_1$ が節を充足することがわかります。

Zero-One Equation (ZOE)

$n$ 個の変数 $x_0, \dots, x_{n-1}\in\{0, 1\}$ に対する、$m$ 個の方程式が与えられます。行列を用いて次のように表現できます。 $$ \def\arraystretch{1.25} \left(\begin{matrix} a_{0, 0} & \dots & a_{0, n-1} \\ \vdots & \ddots & \vdots \\ a_{m-1, 0} & \dots & a_{m-1, n-1} \end{matrix}\right) \left(\begin{matrix} x_0 \\ \vdots \\ x_{n-1} \end{matrix}\right) = \left(\begin{matrix} 1 \\ \vdots \\ 1 \end{matrix}\right) $$ より記号的には、$A = (a_{j, i})_{(j, i)\in\Lambda_m\times\Lambda_n}$ として $A\bm x=\bm1$ とも表せます。ここで、各 $i$, $j$ に対して $a_{i, j}\in\{0, 1\}$ です。与えられた $A$ に対し、$A\bm x=\bm1$ なる $\bm x$ が存在するか？という問題です。

なお、$j$ 番目の方程式は、$S_j = \{i\in\Lambda_n \mid a_{j, i} = 1\}$ として $\sum_{i\in S_j} x_i = 1$ と見なすこともできます。

note: $\sum_{i\in S} x_i = 0$ は、変数 $z$ を導入して $z = 1$ かつ $z + \sum_{i\in S} x_i = 1$ と帰着できます。

Claim 11: ZOE は、3DM から帰着できる。

Proof

3DM の問題例を $\phi = ( (X, Y, Z), T)$ とする。$|X| = n$ かつ $|T| = m$ とし、一般性を失わず $$ \begin{aligned} X &= \{0\}\times\Lambda_n, \\ Y &= \{1\}\times\Lambda_n, \\ Z &= \{2\}\times\Lambda_n, \\ T &= \{(x_j, y_j, z_j) \mid j\in\Lambda_m\} \end{aligned} $$ とする。$3n\times m$ の行列 $A = (a_{i, j})_{(i, j)\in\Lambda_{3n}\times\Lambda_m}$ を $$ a_{i, j} = \begin{cases} 1, & \text{if}\; i-0n\in\Lambda_n \wedge x_j = (0, i); \\ 1, & \text{if}\; i-1n\in\Lambda_n \wedge y_j = (1, i); \\ 1, & \text{if}\; i-2n\in\Lambda_n \wedge z_j = (2, i); \\ 0, & \text{otherwise} \end{cases} $$ で定義する。このとき、ZOE の問題例を $\theta = A$ とすると、$\phi$ が完全マッチングを持つことと $A\bm v=\bm1$ なる $\bm v=(v_0\;\; \cdots\;\; v_{m-1})^{\top}$ が存在することは同値である。

($\implies$): 完全マッチング $M$ が存在するとき、条件を満たす $\bm v$ が存在することを示す。

各 $j\in\Lambda_m$ に対し、$(x_j, y_j, z_j)\in M$ のとき $v_j = 1$、そうでないとき $v_j = 0$ とすると、$A\bm v=\bm1$ を満たす。

To-be-proved 1: 任意の $i\in\Lambda_n$ に対して $\bm a_i\bm v\gt 0$

ある $i\in\Lambda_n$ に対して $\bm a_i\bm v=0$ と仮定する。このとき、 $$ \{(x_j, y_j, z_j)\in M\mid x_j = (0, i)\} = \emptyset $$ となる。これは $M$ が完全マッチングであることに反する。$y_j$ や $z_j$ についても同様。

To-be-proved 2: 任意の $i\in\Lambda_n$ に対して $\bm a_i\bm v\le 1$

ある $i\in\Lambda_n$ に対して $\bm a_i\bm v\gt 0$ を仮定し、同様に矛盾を導ける。

($\impliedby$): 条件を満たす $\bm v$ が存在するとき、完全マッチング $M$ が存在することを示す。

$J = \{j\in\Lambda_m\mid v_j = 1\}$ として $M = \{(x_j, y_j, z_j) \mid j\in J\}$ とする。このとき、$M$ は完全マッチングとなる。各 $i\in\Lambda_n$ に対して $$ \{(x, y, z)\in T\mid x = (0, i)\} = \{(x_j, y_j, z_j)\} $$ が成り立つことが言える。$(1, i)$ や $(2, i)$ についても同様。$\qed$

例

最初に 3DM を導入したときと同様の例を使いましょう。

$$ \begin{aligned} X &= \{0\} \times \Lambda_4, \\ Y &= \{1\} \times \Lambda_4, \\ Z &= \{2\} \times \Lambda_4, \\ T' &= \{(0, 1, 3), (1, 0, 2), (1, 2, 3), (2, 3, 0), (3, 2, 1)\}, \\ T &= \{( (0, x), (1, y), (2, z) )\mid (x, y, z) \in T'\} \end{aligned} $$ に対し、$\phi = ( (X, Y, Z), T)$ を考えます。Claim 11 に従って ZOE の問題例 $\theta$ を構成できます。縦に長すぎます。 $$ \def\arraystretch{1.25} \theta = \left(\begin{array}{ccccc} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \hdashline 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ \hdashline 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 \\ \end{array}\right) $$ 縦に長すぎるため、転置させて書きます。$\bm x=(1\; 1\; 0\; 1\; 1)^{\top}$ が certificate になります。 $$ \def\arraystretch{1.25} \left(\begin{array}{cccc:cccc:cccc} \textcolor{#D3381C}{1}&0&0&0 & 0&\textcolor{#D3381C}{1}&0&0 & 0&0&0&\textcolor{#D3381C}{1} \\ 0&\textcolor{#D3381C}{1}&0&0 & \textcolor{#D3381C}{1}&0&0&0 & 0&0&\textcolor{#D3381C}{1}&0 \\ 0&1&0&0 & 0&0&1&0 & 0&0&0&1 \\ 0&0&\textcolor{#D3381C}{1}&0 & 0&0&0&\textcolor{#D3381C}{1} & \textcolor{#D3381C}{1}&0&0&0 \\ 0&0&0&\textcolor{#D3381C}{1} & 0&0&\textcolor{#D3381C}{1}&0 & 0&\textcolor{#D3381C}{1}&0&0 \end{array}\right)^{\top} \left(\begin{matrix} 1 \\ 1 \\ 0 \\ 1 \\ 1 \end{matrix}\right) $$ 各列について $1$ がちょうど一つずつあることが見て取れます。$\eod$

Maximum 2-SAT (Max 2-SAT)

変数 $x_0, \dots, x_{n-1}\in\{0, 1\}$ を自由に動かせるとき、

$$\phi = \sum_{j=0}^{m-1} {( (x_{l_{j, 0}}\harr a_{j, 0})\vee(x_{l_{j, 1}}\harr a_{j, 1}) )}$$ の最大値を求めよという問題です。 SAT における「（全部は充足できなくても）何々個までの節なら充足できるが...」版と見なすことができます。

Lemma 12: 任意の $\alpha, \beta\in\{0, 1\}$ に対し、下記が成り立つ。 $$ \begin{aligned} \alpha + (\lnot\alpha) &= 1, \\ \alpha\cdot\beta &= \alpha\wedge\beta, \\ \max {\{\alpha, \beta\}} &= \alpha\vee\beta, \\ \alpha + (\lnot\alpha\wedge\beta) &= \alpha\vee\beta, \\ \max {\{\alpha, 1+\beta\}} &= 1+\beta, \\ (\alpha\wedge\beta) + (\alpha\wedge\lnot\beta) &= \alpha, \\ (\alpha\vee\beta) + (\alpha\vee\lnot\beta) &= 1 + \alpha. \end{aligned} $$

Proof

上 4 つは場合分けより明らか。5 つ目は、$\alpha \le 1\le 1+\beta$ に注意せよ。残りは下記の通り。

$$ \begin{aligned} (\alpha\wedge\beta) + (\alpha\wedge\lnot\beta) &= \lnot\alpha\cdot(0+0) + \alpha\cdot(\beta+\lnot\beta) \\ &= \lnot\alpha\cdot 0 + \alpha\cdot 1 \\ &= \alpha, \\ (\alpha\vee\beta) + (\alpha\vee\lnot\beta) &= \lnot\alpha\cdot(\beta+\lnot\beta) + \alpha\cdot(1+1) \\ &= \lnot\alpha\cdot 1 + \alpha\cdot 2 \\ &= (\lnot\alpha) + \alpha + \alpha \\ &= 1 + \alpha. \quad\qed \end{aligned} $$

Lemma 13: 任意の $\alpha\in\{0, 1\}$ と関数 $f\colon\{0, 1\}\to\N$ に対し、 $$f(\alpha) = \lnot\alpha\cdot f(0) + \alpha\cdot f(1)$$ が成り立つ。

Proof. 場合分けより明らか。$\qed$

Lemma 14: 任意の $\alpha, \beta, \gamma, z\in\{0, 1\}$ に対し、 $$ \begin{aligned} &\phantom{{}={}} f(\alpha, \beta, \gamma, z) = {} \\ & \qquad\quad {} (\alpha\vee\beta) + (\alpha\vee\lnot\beta) + (\lnot\alpha\vee\lnot\beta) + (\lnot\alpha\vee z) + (\beta\vee\lnot z) + (\gamma\vee z) \end{aligned} $$ で定義する。このとき、 $$ \max_{z\in\{0, 1\}} f(\alpha, \beta, \gamma, z) = 4 + (\alpha\vee\beta\vee\gamma) $$ が成り立つ。

Proof

$f$ の前半 $3$ 項からなる和は、$z$ によらず下記が成り立つ。 $$ \begin{aligned} &\phantom{{}={}} (\alpha\vee\beta) + (\alpha\vee\lnot\beta) + (\lnot\alpha\vee\lnot\beta) \\ &= \lnot\alpha\cdot(\beta+(\lnot\beta)+1) + \alpha\cdot(1+1+(\lnot\beta) ) \\ &= \lnot\alpha\cdot 2 + \alpha\cdot(2+(\lnot\beta) ) \\ &= ( (\lnot\alpha) + \alpha)\cdot 2 + \alpha\cdot (\lnot\beta) \\ &= 2 + (\alpha\wedge\lnot\beta). \end{aligned} $$ また、後半 $3$ 項からなる和については下記が成り立つ。 $$ \begin{aligned} &\phantom{{}={}} \max_{z\in\{0, 1\}} {(\lnot\alpha\vee z) + (\beta\vee\lnot z) + (\gamma\vee z)} \\ &= \max {\{( (\lnot\alpha) + 1 + \gamma), (1+\beta+1)\}} \\ &= 1 + \max {\{(\lnot\alpha)+\gamma, \beta+1\}} \\ &= 1 + (\lnot\alpha)\cdot(\max {\{1+\gamma, \beta+1\}}) + \alpha\cdot(\max {\{0+\gamma, \beta+1\}}) \\ &= 1 + (\lnot\alpha)\cdot(1 + (\beta\vee\gamma) ) + \alpha\cdot(1 + \beta) \\ &= 1 + ( (\lnot\alpha) + \alpha) + (\lnot\alpha)\cdot(\beta\vee\gamma) + \alpha\cdot\beta \\ &= 2 + (\lnot\alpha\wedge(\beta\vee\gamma) ) + (\alpha\wedge\beta). \\ \end{aligned} $$ 以上より、下記を得る。 $$ \begin{aligned} \max_{z\in\{0, 1\}} f(\alpha, \beta, \gamma, z) &= 2 + (\alpha\wedge\lnot\beta) + 2 + (\lnot\alpha\wedge(\beta\vee\gamma) ) + (\alpha\wedge\beta) \\ &= 4 + (\alpha\wedge\beta) + (\alpha\wedge\lnot\beta) + 2 + (\lnot\alpha\wedge(\beta\vee\gamma) ) \\ &= 4 + \alpha + (\lnot\alpha\wedge(\beta\vee\gamma) ) \\ &= 4 + \alpha\vee(\beta\vee\gamma) \\ &= 4 + (\alpha\vee\beta\vee\gamma). \quad\qed \end{aligned} $$

Claim 15: Max 2-SAT は 3-SAT から帰着できる。

Proof

3-SAT の問題例を $$ \phi = \bigwedge_{j=0}^{m-1} {(\alpha_{j, 0}\vee\alpha_{j, 1}\vee\alpha_{j, 2})} $$ とし、$n$ 個の変数からなるとする。これに対し、Claim 14 で定義した $f$ と新たに導入する変数 $z_0, \dots, z_{m-1}$ を用いて $$ \theta = \sum_{j=0}^{m-1} f(\alpha_{j, 0}, \alpha_{j, 1}, \alpha_{j, 2}, z_j) $$ で定義する。このとき、ある列 $\bm x = (x_0, \dots, x_{n-1})$ および $\bm z = (z_0, \dots, z_{m-1})$ に対して $\theta(\bm x, \bm z) \ge 5m$ が成り立つことと $\phi(\bm x) = 1$ であることは同値である。

$$ \begin{aligned}\ \max_{\bm x, \bm z} \theta &= \max_{\bm x, \bm z} \sum_{j=0}^{m-1} f(\alpha_{j, 0}, \alpha_{j, 1}, \alpha_{j, 2}, z_j) \\ &= \max_{\bm x} \sum_{j=0}^{m-1} {(4+(\alpha_{j, 0}\vee\alpha_{j, 1}\vee\alpha_{j, 2}) )} \\ &= 4m + \max_{\bm x} \sum_{j=0}^{m-1} {(\alpha_{j, 0}\vee\alpha_{j, 1}\vee\alpha_{j, 2})} \\ \end{aligned} $$ である。

($\implies$): 対偶 $\phi(\bm x) = 0 \implies \max_{\bm z} \theta(\bm x, \bm z) \lt 5m$ を示す。

ある $j$ が存在して $(\alpha_{j, 0}\vee\alpha_{j, 1}\vee\alpha_{j, 2}) = 0$ が成り立つため、 $$ \max_{\bm z} {\theta(\bm x, \bm z)} = 4m + \sum_{j=0}^{m-1} {(\alpha_{j, 0}\vee\alpha_{j, 1}\vee\alpha_{j, 2})} \lt 4m + m = 5m $$ となる。

($\impliedby$): $\phi(\bm x) = 1 \implies \max_{\bm z} \theta(\bm x, \bm z) \ge 5m$ を示す。

任意の $j$ に対して $(\alpha_{j, 0}\vee\alpha_{j, 1}\vee\alpha_{j, 2}) = 1$ が成り立つため、 $$ \max_{\bm z} {\theta(\bm x, \bm z)} = 4m + \sum_{j=0}^{m-1} {(\alpha_{j, 0}\vee\alpha_{j, 1}\vee\alpha_{j, 2})} = 4m + m \ge 5m $$ となる。$\qed$

上記の $f(\alpha, \beta, \gamma, z) = 4 + (\alpha\vee\beta\vee\gamma)$ なる gadget は全探索により探しました。一つの節に重複するリテラルが登場することを許すなら、下記の方が少ない個数で済みます。

Claim 16: 以下で $g(\alpha, \beta, \gamma, z)$ を定義する。 $$ g(\alpha, \beta, \gamma, z) = (\alpha\vee\beta)+(\lnot\alpha\vee\lnot z)+(\lnot\beta\vee\lnot z)+(\gamma\vee\lnot z)+(z\vee z). $$ これに対し、 $$ \max_{z\in\{0, 1\}} g(\alpha, \beta, \gamma, z) = 3 + (\alpha\vee\beta\vee\gamma) $$ が成り立つ。

Proof

$$ \begin{aligned} \max_{z\in\{0, 1\}} g(\alpha, \beta, \gamma, z) &= (\alpha\vee\beta) + \max {\{1+1+1+0, \lnot\alpha+\lnot\beta+\gamma+1\}} \\ &= (\alpha\vee\beta) + \max {\{3, 1+(\lnot\alpha+\lnot\beta+\gamma)\}} \\ &= \lnot(\alpha\vee\beta)\cdot(\max {\{3, 1+(1+1+\gamma)\}}) \\ & \qquad\quad {} + (\alpha\vee\beta)\cdot(1 + \max {\{3, 1+(\lnot\alpha+\lnot\beta+\gamma)\}}) \\ &= \lnot(\alpha\vee\beta)\cdot(3+\gamma) + (\alpha\vee\beta)\cdot(1 + 3) \\ &= 3 + \lnot(\alpha\vee\beta)\wedge\gamma + (\alpha\vee\beta) \\ &= 3 + (\alpha\vee\beta\vee\gamma). \quad\qed \end{aligned} $$

帰着②

読者への課題パートです。概要だけ述べます。

Directed Hamiltonian Cycle

有向グラフ $G = (V, E)$ が与えられます。すべての頂点をちょうど一回ずつ通るサイクルはあるか？という問題です。すなわち、頂点集合 $V$ の並べ替えによって得られる列 $(v_0, \dots, v_{|V|-1})\in V!$ であって、任意の $i\in\Lambda_{|V|-1}$ に対して $(v_i, v_{i+1})\in E$ かつ $(v_{|V|-1}, v_0)\in E$ を満たすものは存在するか？という問題です。このサイクルを Hamiltonハミルトンサイクル (Hamiltonian cycle) と呼びます。

例

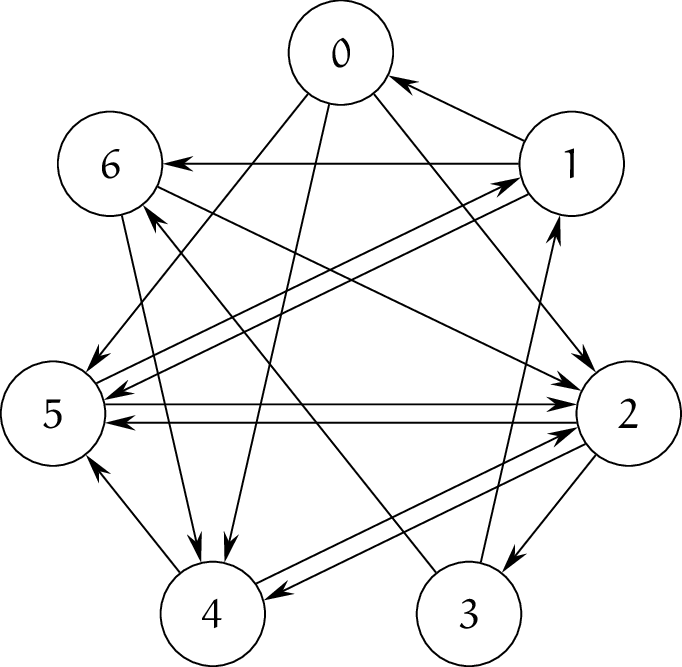
次の $7$ 頂点のグラフ $G$ に対して、Hamiltonian Cycle の問題例 $\phi = G$ を考えます。

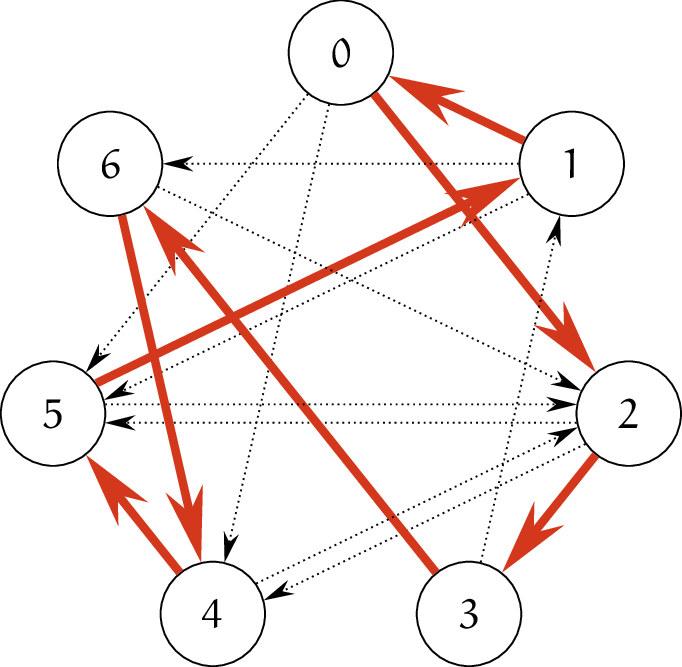
Hamiltonian cycle は存在し、次が certificate となります。

この例においては、列の始点の違いを同一視すると一意です。$\eod$

Claim 17: Directed Hamiltonian Cycle は 3-SAT から帰着できる。

Reduction + Sketch

$i$ 番目の変数 ($i\in\Lambda_n$) に対応する gadget を $$ \begin{aligned} V_{\text{variable}}(i) &= \{i\}\times\Lambda_{3(m+1)}, \\ % E_{\text{variable}}(i) &= \left\{\bigl( (i, j), (i, j+1) \bigr) \bigm| j\in\Lambda_{3(m+1)-1}\right\}, \\ E_{\text{variable}}(i) &= \left\{\bigl( (i, j), (i, j')\bigr) \in {V_{\text{variable}}(i)}^2 \bigm| |j-j'|=1\right\}, \\ &= \bigcup_{j\in\Lambda_{3(m+1)-1}} \left\{\bigl( (i, j), (i, j+1) \bigr), \bigl( (i, j+1), (i, j) \bigr)\right\} \end{aligned} $$ で定義する。また、$V_{\text{variable}}(i)$ のうち $j$ 番目の節 ($j\in\Lambda_m$) に対応する要素を得る関数を $$ \begin{aligned} f_{\text{out}}(i, j, a) &= \bigl(i, 3(j+1)+(1-a)\bigr), \\ f_{\text{in}}(i, j, a) &= \bigl(i, 3(j+1)+a\bigr) \end{aligned} $$ で定義する。$j$ 番目の節 ($j\in\Lambda_m$) に対応する頂点を $v_j$ とし、これを含む gadget を $$ \begin{aligned} E_{\text{clause}}(j) &= \bigcup_{k\in\Lambda_3} \left\{ \bigl(f_{\text{out}}(l_{j, k}, j, a_{j, k}), v_j\bigr), \bigl(v_j, f_{\text{in}}(l_{j, k}, j, a_{j, k})\bigr) \right\} \end{aligned} $$ で定義する。

さらに、超頂点 $v_{\text{source}}$, $v_{\text{sink}}$ を導入する。また、$V_{\text{variable}}(i)$ の両端の要素を得る関数を $$ g_{\text{ends}}(i) = \{i\} \times \{0, 3(m+1)-1\} $$ で定義する。これらの要素における辺集合を $$ \begin{aligned} E_{\text{outer}} &= \bigl(\{v_{\text{source}}\}\times g_{\text{ends}}(0)\bigr) \\ &\qquad\quad {} \cup \left(\bigcup_{i\in\Lambda_{n-1}} g_{\text{ends}}(i) \times g_{\text{ends}}(i+1)\right) \cup \bigl(g_{\text{ends}}(n-1)\times\{v_{\text{sink}}\}\bigr) \end{aligned} $$ で定義する。

これらを用いて $$ \begin{aligned} V &= \{v_{\text{source}}, v_{\text{sink}}\}\cup\{v_i\mid i\in\Lambda_n\}\cup V_{\text{variable}}(i), \\ E &= \left(\bigcup_{i\in\Lambda_n} E_{\text{variable}}(i)\right) \cup \left(\bigcup_{j\in\Lambda_m} E_{\text{clause}}(j)\right) \cup E_{\text{outer}} \end{aligned} $$ とし、$\theta = (V, E)$ とする。$\theta$ における Hamilton サイクルの存在性が $\phi$ の充足可能性と同値になる。

($\implies$): $\theta$ の Hamiltonian サイクルから $\phi(\bm x)=1$ なる $\bm x$ を構成できることを示す。

$\theta$ の certificate が含む辺全体から集合を $P$ とする。$\bigl( (i, 0), (i, 1) \bigr)\in P$ のとき $x_i = 1$ とする。そうでないとき $\bigl( (i, 1), (i, 0)\bigr)\in P$ であり、このとき $x_i = 0$ とする。

Lemma: $\bigl( (i, 0), (i, 1)\bigr)\in P$ のとき、$\bigl( (i, j), (i, j')\bigr)\in P$ ならば $j\lt j'$ が成り立つ。

Lemma: $\bigl( (i, 1), (i, 0)\bigr)\in P$ のとき、$\bigl( (i, j), (i, j')\bigr)\in P$ ならば $j\gt j'$ が成り立つ。

Lemma: $(f_{\text{out}}(i, j, a), v_j)\in P$ と $(v_j, f_{\text{in}}(i, j, a) )\in P$ は同値である。

これらを踏まえると、頂点 $v_j$ を通るならば節 $j$ が充足することを示せるはず。

($\impliedby$): $\phi(\bm x)=1$ なる $\bm x$ から $\theta$ の Hamilton サイクルを構成できることを示す。

グラフの構成から容易であるはず。$\eod$

例

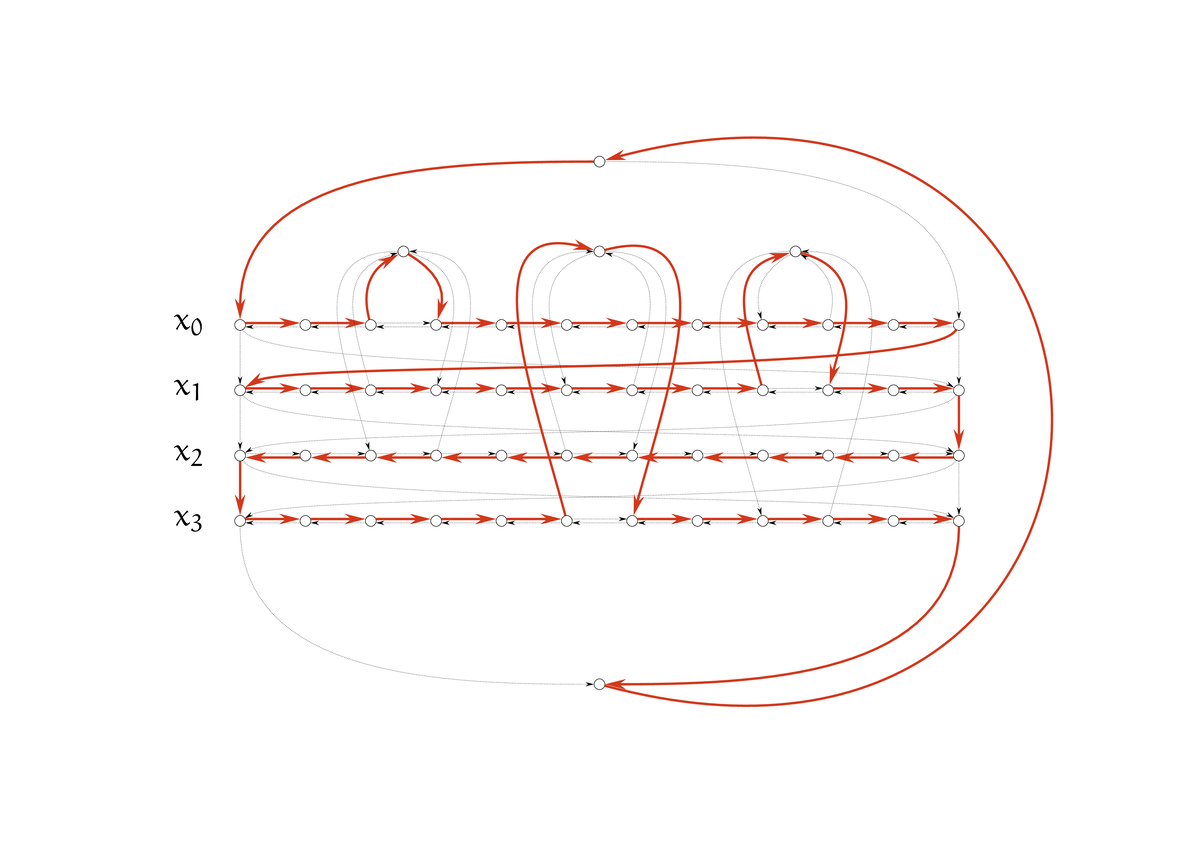
問題例 $$ \phi = (x_0\vee x_1\vee \lnot x_2) \wedge (\lnot x_1\vee x_2\vee x_3) \wedge (\lnot x_0\vee x_1\vee \lnot x_3) $$ で考えます。

一番上と一番下の頂点がそれぞれ $v_{\text{source}}$ と $v_{\text{sink}}$ です。$v_{\text{source}}$ と $x_0$ の段の間にある頂点が、左から $v_0$, $v_1$, $v_2$ です。certificate は次のようになります。

$i$ 行目が右に進んでいれば $x_i = 1$、左に進んでいれば $x_i = 0$ というイメージです。$x_i$ が節 $j$ を充足するためには、$i$ 行目の進行方向と $f_{\text{out}}(i, j, a) \rightsquigarrow v_j \rightsquigarrow f_{\text{in}}(i, j, a)$ の方向が一致している必要があります。

$f_{\text{out}}(i, j, a)\rightsquigarrow v_j\rightsquigarrow f_{\text{in}}(i, j, a)$ がなす gadget の両端の頂点は必要なのか？と思う人がいるかもしれません。えびちゃんは最初思いました。

反例

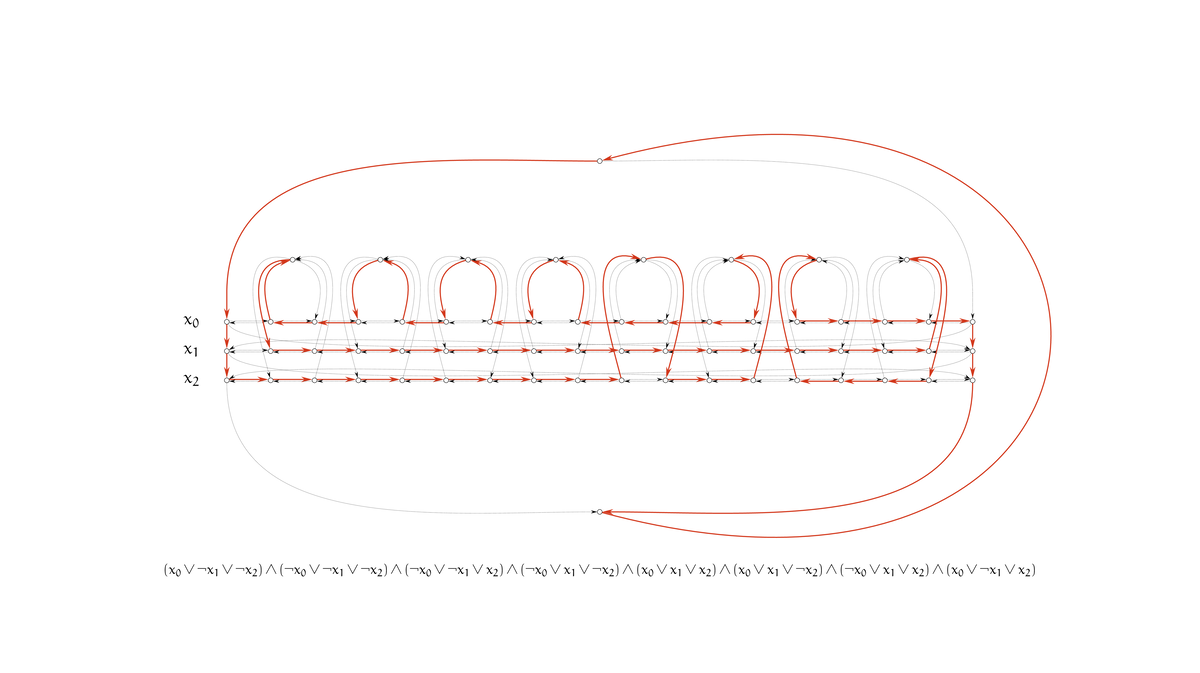
変数が $2$ 個以下や節が $7$ 個以下の場合の 3-SAT は必ず充足可能なので、これが最小反例です。手で求めるのはたいへんだったので、TSP に帰着して TSP solver (elkai-rs) に投げて、適当な certificate を出させました。ハチャメチャな Hamiltonian cycle を出してくれるかはお祈りでしたが、うまくいきました。 $$ \bigwedge_{j=0}^7 {(x_0\harr 0)\vee(x_0\harr 1)\vee(x_1\harr 0)\vee(x_1\harr 1)\vee(x_2\harr 0)\vee(x_2\harr 1)} $$ に相当するグラフで TSP を求め、辻褄が合うような 3-SAT を構成しました。

正しい帰着においては、$i$ 行目で右に進んでいれば $x_i=1$、$i$ 行目で左に進んでいれば $x_i=0$ ですが、このグラフでは右に進んだり左に進んだりしています。それぞれの節で $x_i=0$ と $x_i=1$ の都合のいい方を選べてしまっては不都合なので、それを防ぐ必要があります。

また、この反例に使った 3-SAT は、$(x_0)\wedge(\lnot x_0)$ を 3-SAT になるように変形したものに相当します。$\eod$

$\eod$

Undirected Hamiltonian Cycle

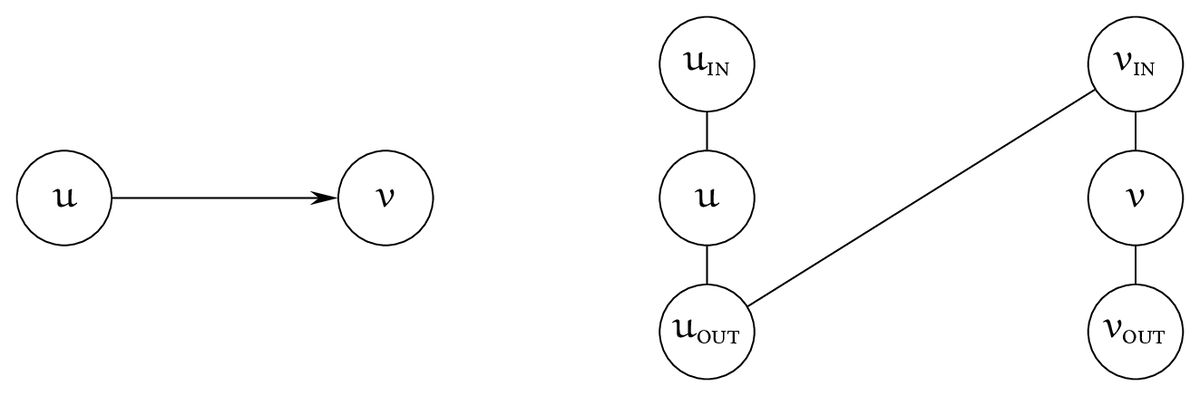
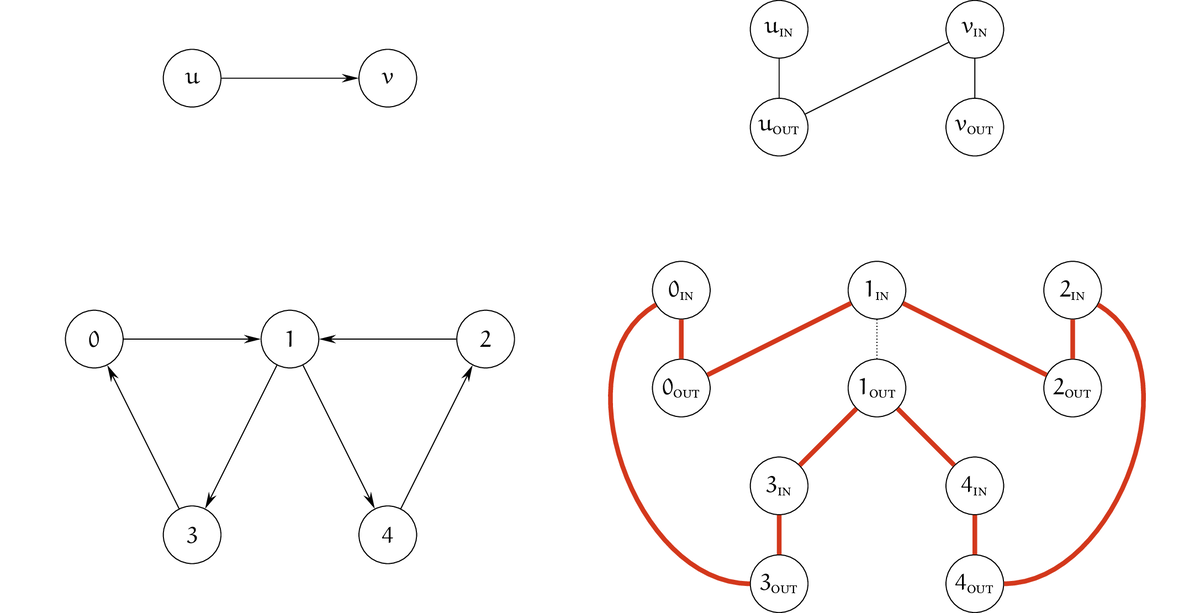
無向グラフ版の Hamiltonian Cycle です。次の one-way gadget を用いて、Directed Hamiltonian Cycle から帰着できます。

各 $v$ に対応する頂点は、$(v_{\textsc{in}}, v, v_{\textsc{out}})$ ではなく $(v_{\textsc{in}}, v_{\textsc{out}})$ ではだめか？

exercise: より小さい反例を構成せよ。$\eod$

note: 同じ辺を複数回使ってもよいと思います。$V = \{0, 1\}$ かつ $E = \{\{0, 1\}\}$ に対して、$(0, 1)$ は条件を満たしていると思います。

Traveling Salesperson Problem

有向グラフ $G = (V, E)$ と辺の重み関数 $w\colon E\to\Z$ が与えられます。$|V| = n$ とします。頂点集合 $V$ の並べ替えによって得られる列 $\bm v = (v_0, \dots, v_{n-1})$ であって、各 $i\in\Lambda_n$ に対して $(v_i, v_{(i+1)\bmod n})\in E$ であるものに対し、 $$ f(\bm v) = \sum_{i=0}^{n-1} w( (v_i, v_{(i+1)\bmod n}) ) $$ の最小値を求める問題です。決定問題版は、整数 $k$ も与えられて $f(\bm v)\le k$ にできるか？です。

Hamilton Cycle からそのまま帰着できます。各 $e\in E$ に対して $w(e) = 1$ として $\theta = ( (V, E), w)$ の certificate をそのまま $\phi$ の certificate にできます。

また、無向グラフ版についても同様に定義できます。

Maximum Cut (Max Cut)

無向グラフ $G = (V, E)$ が与えられます。$S\subseteq V$ に対し、 $$ \delta(S) = \{\{u, v\}\in E\mid (u\in S)\Longleftrightarrow(v\notin S)\} $$ を $S$ による カット集合 (cut-set) と呼びます。また、$(S, V\smallsetminus S)$ を カット (cut) と呼びます。カット集合の要素数が最大となるカット（またはその最大値）を求めよという問題です。

決定問題版はいつものように定義します。

余談

競プロ界隈においては、最大フロー問題の双対として最小カット問題が有名です。特に、「頂点 $s$ から $t$ に到達できないようにするには辺を何本切ればよいか？」という問題文として広く認知されています。そのため、最大カットの話をすると「全部の辺を切るギャグですか？笑」となるのがありがちです。カットと呼んでいるものの定義に気をつけましょう。$\eod$

Claim 18: Maximum Cut は Maximum Independent Set から帰着できる。

Proof

MIS の問題例を $\phi = ( (V, E), k)$ とする。このとき、以下で定義される Maximum Cut の問題例 $\theta = ( (V', E'), k')$ に帰着できる。

$$ V_E = \bigcup_{e = \{u, v\} \in E} {\{e_u, e_v\}} $$ とする。ここで、$e_v = (e, v)$ とする。また、$x\notin V$ を導入し、$V' = V \cup V_E\cup \{x\}$ とする。

$E_x = \{ \{x, v\} \mid v\in V\}$ とする。また、各 $e = \{u, v\}\in E$ に対し $$ E_e = \bigl\{\{u, e_u\}, \{x, e_u\}, \{v, e_v\}, \{x, e_v\}, \{e_u, e_v\}\bigr\} $$ とする。これを用いて $$ E' = E_x \cup \left(\bigcup_{e\in E} E_e\right) $$ とする。また、$k' = k + 4 \, |E|$ とする。

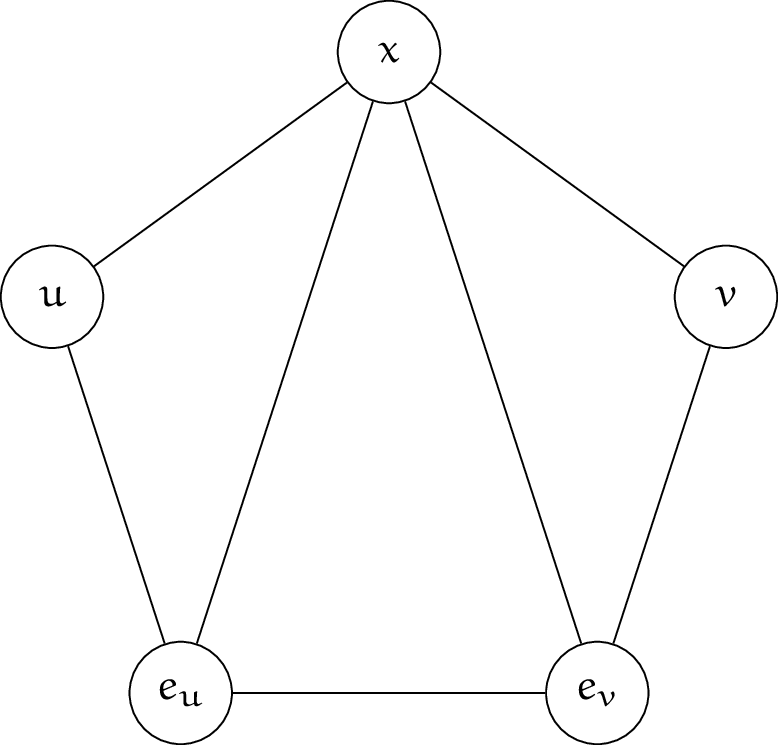
($\implies$): $(V, E)$ の独立集合 $I$ から、$(V', E')$ におけるサイズ $|I|+4\, |E|$ のカット $S$ を構成する。

下図は、上の段から順に $u\notin S\wedge v\notin S$、$u\in S\wedge v\notin S$、$u\in S\wedge v\in S$ のときの、$E_x$ と $E_e$ のカット集合のサイズへの寄与である。対称なものを除いたすべての組合せを記載した。黒い頂点が $S$ に含まれることを表す。

$S \cap V = I$ とする。各 $e$ に対して独立に選択できるため、$e_u$ と $e_v$ を適切に選択することで $E_e$ から $4$ の寄与をすることができる。よって、$|S| = |I| + 4\,|E|$ となる。

($\impliedby$): $(V', E')$ におけるサイズ $k+4\, |E|$ のカット $S$ が存在するとき、$(V, E)$ におけるサイズ $k$ の独立集合 $I$ が存在することを示す。

一般性を失わず $x\notin S$ とする。

$J = S \cap V$ とする。$J$ に含まれる頂点同士を結ぶ辺全体からなる集合を $E_J$ とする。すなわち、 $$ E_J = \bigl\{ \{u, v\} \in E \bigm| u\in J \wedge v\in J\bigr\} $$ とする。このとき、上記の寄与の表から $$ \begin{aligned} |\delta(S)| &\le |J| + 3\, |E_J| + 4\,|E\smallsetminus E_J| \\ &= |J| + 3\, |E_J| + 4\,|E| - 4\,|E_J| \\ &= |J| + 4\,|E| - |E_J| \end{aligned} $$ となる。前提より $|\delta(S)| \ge k+4\,|E|$ であるから $k+4\,|E| \le |J| + 4\,|E|-|E_J|$ であり、$|J| \ge k+|E_J|$ が従う。

Lemma: 任意のグラフ $G = (V, E)$ と非負整数 $k$ に対して、$G$ は少なくとも $\max{\{0, |V|-|E|\}}$ 個の連結成分を持つ。

Lemma: 任意のグラフ $G = (V, E)$ と非負整数 $k$ に対して、$|V| \ge k+|E|$ ならば $G$ は少なくとも $k$ 個の連結成分を持つ。

Lemma: 任意のグラフ $G$ と非負整数 $k$ に対して、$G$ が少なくとも $k$ 個の連結成分を持つならば、$G$ はサイズ $k$ の独立集合を持つ。

以上より $J$ はサイズ $k$ の独立集合を持つ。$\qed$

$\gdef\nae{\textsc{nae}}$

他にも、$\nae(x_0, \dots, x_{k-1}) = \lnot( (x_0\harr x_1) \wedge\dots\wedge (x_{k-2}\harr x_{k-1}) )$ で定義される NAE 演算 (not-all-equal) を用いて $$ \bigwedge_{j=0}^{k-1} {\nae(x_{l_{j, 0}}, x_{l_{j, 1}}, x_{l_{j, 2}})} $$ の形式で表される 3-NAE SAT から帰着することで示す方法もあるらしいです。3-CNF SAT → 4-NAE SAT → 3-NAE SAT → Max Cut と帰着できるらしいです。

Integer Linear Programming (ILP)

行列 $A = (a_{j, i})_{(j, i)\in\Lambda_m\times\Lambda_n}\in\Z^{m\times n}$ とベクトル $\bm b \in\Z^m$, $\bm c \in\Z^n$ が与えられます。これに対し、$A \bm x \le \bm b$ を満たす $\bm x \in\Z^n$ における $\bm c^{\top}\bm x$ の最大値を求めよという問題です。ただし、$A\bm x\le \bm b$ は、各 $j\in\Lambda_m$ に対して $\bm a_j\bm x\le b_j$ として定義します。なお、$A\bm x\le \bm b$ を満たす $\bm x$ が存在しない場合は $-\infty$、$\bm c^{\top}\bm x$ が有界でない場合は $+\infty$ を答えるとします。 整数計画問題 (integer linear programming) と呼ばれます。

決定問題版は、整数 $k$ も与えられて $\bm c^{\top}\bm x\ge k$ なる $\bm x$ が存在するか？です。

$$ \begin{aligned} &\phantom{{}\iff{}} x_i \in \{0, 1\} \\ &\iff (x_i\ge 0) \wedge (x_i\le 1) \\ &\iff ( (-1)\cdot x_i\le 0) \wedge (1\cdot x_i\le 1), \\ &\phantom{{}\iff{}} \sum_{i=0}^{n-1} a_i x_i = 1 \\ &\iff \left(\sum_{i=0}^{n-1} a_i x_i \le 1\right) \wedge \left(\sum_{i=0}^{n-1} a_i x_i \ge 1\right) \\ &\iff \left(\sum_{i=0}^{n-1} a_i x_i \le 1\right) \wedge \left(\sum_{i=0}^{n-1} {(-a_i) x_i} \le -1\right) \end{aligned} $$ より、ZOE の制約を表現できます。$\bm c^{\top}\bm x\ge 0$ あるいは $\bm c^{\top}\bm x\gt -\infty$ などとして判定すればよいです。

また、SAT からも自然に帰着できます。SAT の問題例を $$ \phi = \bigwedge_{j=0}^{m-1} \bigvee_{k=0}^{c_j-1} {(x_{l_{j, k}}\harr a_{j, k})} % {( (x_{l_{j, 0}}\harr a_{j, 0})\wedge(x_{l_{j, 1}}\harr a_{j, 1})\wedge(x_{l_{j, 2}}\harr a_{j, 2}) )} $$ とします。$2n$ 個の変数 $x_0, \dots, x_{2n-1}$ からなる ILP の問題例 $\theta$ を下記で定義すればよいです。$x_{n+i}$ が $\lnot x_i$ に相当しています。 $$ \theta = \left\{\;\begin{aligned} x_i &\ge 0 && (i\in\Lambda_{2n}), \\ x_i + x_{n+i} &= 1 && (i\in\Lambda_n), \\ \sum_{k=0}^{c_j-1} x_{(1-a_{j, k})n + l_{j, k}} &\ge 1 && (j\in\Lambda_m). \end{aligned}\right. $$

Minimum Vertex Cover

無向グラフ $G = (V, E)$ が与えられます。$S\subseteq V$ であって、任意の $\{u, v\}\in E$ に対して $u\in S$ または $v\in S$ を満たすものを 頂点被覆 (vertex cover) と呼びます。要素数が最小となる頂点被覆（または要素数の最小値）を求めよという問題です。

決定問題版は、要素数 $k$ 以下の頂点被覆が存在するか？です。

Lemma 19: $S$ が $G$ の頂点被覆であるとき、$V\smallsetminus S$ は $G$ における独立集合となる。

Proof

$\bar S = V\smallsetminus S$ とする。頂点被覆の定義より、任意の $\{u, v\}\in E$ に対して $$ \begin{aligned} (u\in S) \vee (v\in S) &\iff (u\notin \bar S) \vee (v\notin \bar S) \\ &\iff \lnot ( (u\in \bar S) \wedge (v\in \bar S) ) \end{aligned} $$ が成り立つ。すなわち、$u, v\in \bar S$ かつ $\{u, v\}\in E$ なる $(u, v)\in V^2$ は存在しない。よって、任意の $u, v\in\bar S$ に対して $\{u, v\}\notin E$ であるから、$\bar S$ は独立集合である。$\qed$

以上より、独立集合から帰着できます。

Minimum Set Cover

集合 $S$ と、その部分集合族 $\mathscr S\subseteq 2^S$ が与えられます。部分集合族 $\mathscr T\subseteq \mathscr S$ であって、以下の条件を満たすものを 集合被覆 (set cover) と呼びます。 $$ \bigcup_{T\in \mathscr T} T = S. $$ 最小の要素数の $\mathscr T$ を求めよという問題です。決定問題版はいつものように定義できます。

Vertex Cover を部分問題として持ちます。 $S = E$ とし、 $$ \begin{aligned} S_v &= \{e\in E \mid v\in e\}, \\ \mathscr S &= \{ S_v \mid v\in V\} \end{aligned} $$ として帰着できます。

Exact Cover

Set Cover の問題設定において、各 $T_i, T_j \in \mathscr T$ について $T_i \ne T_j$ ならば $T_i\cap T_j = \emptyset$ を満たすものが存在するか？という問題です。

ZOE から帰着できます。サイズ $k$ の exact Cover があってもサイズ $k\pm 1$ の exact cover についてはなんとも言えないので、Minimum Exact Cover とか Maximum Exact Cover とかはもっと難しい気がします。ほんとかな？最小・最大の問題設定が言及されているの自体あまり見かけませんでした。

Hamiltonian Path

Hamiltonian Cycle の問題設定から $(v_{n-1}, v_0)\in E$ の条件を除いたものです。有向版と無向版をそれぞれ定義できます。

有向版は Hamiltonian Cycle と同様にして 3-SAT から帰着できます。無向版は有向版から帰着できます。

Longest Path

グラフ $G = (V, E)$ が与えられ、パスの長さの最大値を求める問題です。決定問題版は、長さ $k$ 以上のパスが存在するか？です。

$k = |V|-1$ として、Hamiltonian Path から帰着できます。

Maximum Clique

無向グラフ $G = (V, E)$ が与えられます。$S\subseteq V$ であって、任意の $u, v \in S$ ($u\ne v$) について $\{u, v\}\in E$ を満たすものを クリーク (clique) と呼びます。要素数が最大となるクリーク（あるいは要素数の最大値）を求めよという問題です。

決定問題版は、$|S| \ge k$ なるクリークが存在するか？を判定します。 $$\bar E = \bigl\{\{u, v\}\bigm| (u, v)\in V^2\bigr\} \smallsetminus E$$ として、グラフ $(V, \bar E)$ においてサイズ $k$ の独立集合が存在することと同値です。

Minimum Dominating Set

無向グラフ $G = (V, E)$ が与えられます。$S\subseteq V$ であって、任意の $v\in V\smallsetminus S$ に対して、ある $u\in S$ が存在して $\{u, v\}\in E$ が成り立つものを 支配集合 (dominating set) と呼びます。要素数が最小となる支配集合（または要素数の最小値）を求めよという問題です。

決定問題版は、要素数 $k$ 以下の支配集合が存在するか？です。

Set Cover から帰着できます。

Subset Sum Problem

長さ $n$ の整数列 $A = (a_0, \dots, a_{n-1})$ と整数 $k$ が与えられます。添字 $I\subseteq\Lambda_n$ であって、$\sum_{i\in I} a_i = k$ なる $I$ が存在するか？という問題です。部分和問題 (subset sum problem) と呼ばれます。

Claim 20: Subset Sum Problem は 3-SAT から帰着できる。

Reduction + Sketch

3-SAT の問題例を $$ \phi = \bigwedge_{j=0}^{m-1} \bigvee_{k=0}^2 {(x_{l_{j, k}} \harr a_{j, k})} $$ とする。ここで $(l_{j, k}, a_{j, k})\in\Lambda_n\times\{0, 1\}$ とする。また、 $$ \begin{aligned} S_{i, 0} &= \bigl\{ j\in\Lambda_m \bigm| (i, 0)\in \{(l_{j, k}, a_{j, k}) \mid k\in\Lambda_3 \} \bigr\}, \\ S_{i, 1} &= \bigl\{ j\in\Lambda_m \bigm| (i, 1)\in \{(l_{j, k}, a_{j, k}) \mid k\in\Lambda_3 \} \bigr\} \end{aligned} $$ とする。直感的には、$S_{i, 0}$ は $\lnot x_i$ が含まれる節の番号全体からなる集合、$S_{i, 1}$ は $x_i$ が含まれる節の番号全体からなる集合に対応する。

各 $i\in\Lambda_n$ に対し $$ \begin{aligned} b_{2i+0} &= 10^{m+n-1+i} + \sum_{j\in S_{i, 0}} 10^{m-1+j}, \\ b_{2i+1} &= 10^{m+n-1+i} + \sum_{j\in S_{i, 1}} 10^{m-1+j} \end{aligned} $$ とし、また各 $j\in\Lambda_m$ に対し $$ b_{2n+2j+0} = b_{2n+2j+1} = 10^{m-1+j} $$ とする。また、 $$ \begin{aligned} z &= 10^m\cdot\sum_{i=0}^{n-1} 10^i + \sum_{j=0}^{m-1} 3\cdot 10^j \\ &= 10^m\cdot\frac{10^n-1}9 + \frac{10^m-1}3 \\ &= \underbrace{11\dots1}_{n}\, \underbrace{33\cdots 3}_{m} \end{aligned} $$ とする。

$B = (b_0, \dots, b_{2n+2m})$ として、$\theta = (B, z)$ における部分和問題の解の存在性が $\phi$ の充足可能性と同値となる。

($\implies$): $2i+0\in I$ のとき $x_i = 0$、$2i+1\in I$ のとき $x_i = 1$ とすればよい。

($\impliedby$): 各 $i$ に対して $x_i = 0$ のときは $2i+0\in I$、$x_i = 1$ のときは $2i+1\in I$ とする。また、$i\ge 2n$ については（桁ごとに独立に決められるため）適切に定めればよい。 $\eod$

例

$$ \phi = (x_0\vee x_1\vee\lnot x_2)\wedge(\lnot x_1\vee x_2\vee x_3)\wedge(\lnot x_0\vee x_1\vee\lnot x_3) $$ とすると、 $$ \begin{aligned} b_0 &= 1000001, \\ b_1 &= 1000100, \\ b_2 &= 0100010, \\ b_3 &= 0100101, \\ b_4 &= 0010100, \\ b_5 &= 0010010, \\ b_6 &= 0001001, \\ b_7 &= 0001010, \\ b_8 &= 0000100, \\ b_9 &= 0000100, \\ b_{10} &= 0000010, \\ b_{11} &= 0000010, \\ b_{12} &= 0000001, \\ b_{13} &= 0000001, \\ z &= 1111333 \end{aligned} $$ となる。たとえば $I = \{1, 2, 5, 6, 8, 9, 10, 12, 13\}$ とすることで $\sum_{j\in I} b_j = z$ とできる。 $$ \begin{aligned} \gdef\zero{\textcolor{#CCC}{0}} \gdef\one{\textcolor{#D3381C}{1}} b_1 &= \one\zero\zero\zero\one\zero\zero, \\ b_2 &= \zero\one\zero\zero\zero\one\zero, \\ b_5 &= \zero\zero\one\zero\zero\one\zero, \\ b_6 &= \zero\zero\zero\one\zero\zero\one, \\ b_8 &= \zero\zero\zero\zero\one\zero\zero, \\ b_9 &= \zero\zero\zero\zero\one\zero\zero, \\ b_{10} &= \zero\zero\zero\zero\zero\one\zero, \\ b_{12} &= \zero\zero\zero\zero\zero\zero\one, \\ b_{13} &= \zero\zero\zero\zero\zero\zero\one. \end{aligned} $$ これは $\bm x = (1, 0, 1, 0)$ に対応する。$\eod$

Knapsack Problem

長さ $n$ の整数列 $A = (a_0, \dots, a_{n-1})$, $B = (b_0, \dots, b_{n-1})$ と整数 $k_A$, $k_B$ が与えられます。添字 $I\subseteq\Lambda_n$ であって、$\sum_{i\in I} a_i \le k_A$ かつ $\sum_{i\in I} b_i \ge k_B$ なる $I$ が存在するか？という問題です。

各 $i\in\Lambda_n$ について $a_i = b_i$ とし、また $k_A = k_B = k$ とすることにより、部分和問題から帰着できます。

おまけ

TM からの帰着

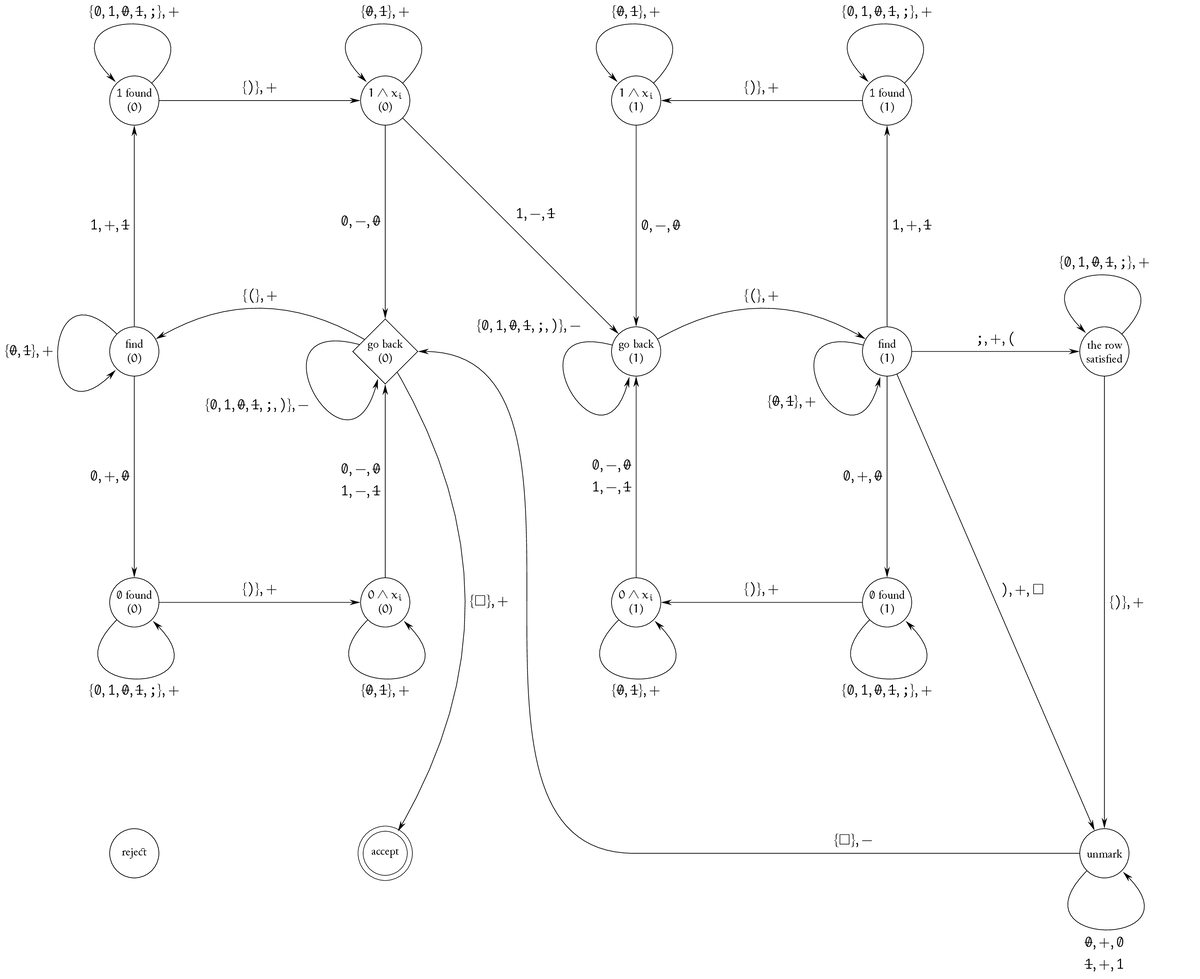
ZOE の検証器の TM を考えます。入力として $$ \texttt{\char40}a_{0, 0}\dots a_{0, n-1}\texttt{;}\dots\texttt{;}a_{m-1, 0}\dots a_{m-1, n-1}\texttt{\char41}x_0\dots x_{n-1} $$ を与えると、$A\bm x=\bm1$ のときに受理し、そうでないときに拒否します。ここでは、入力形式が不正な場合についてはあまり考えていません。

大まかな挙動は次のようなものに相当します。

各 $j$ に対して下記を行う
- 各 $i$ に対して下記を行う
  - $a_{j, i}$ と $x_i$ を比較する
  - $a_{j, i} \wedge x_i = 1$ ならば下記を行う
    - すでに $a_{j, i'} \wedge x_{i'} = 1$ なる $i'\lt i$ を見つけているなら拒否する
- $a_{j, i} \wedge x_i = 1$ なる $i$ が見つからなければ拒否する
受理する

$i$ や $j$ を値として持っておいても使いにくいため、「ここまでは見たよ〜」というマークをつけるような動きにしています。 $a_{j, i} \wedge x_i = 1$ なる $i$ を見つけたかどうかは、TM の状態として保持しています。

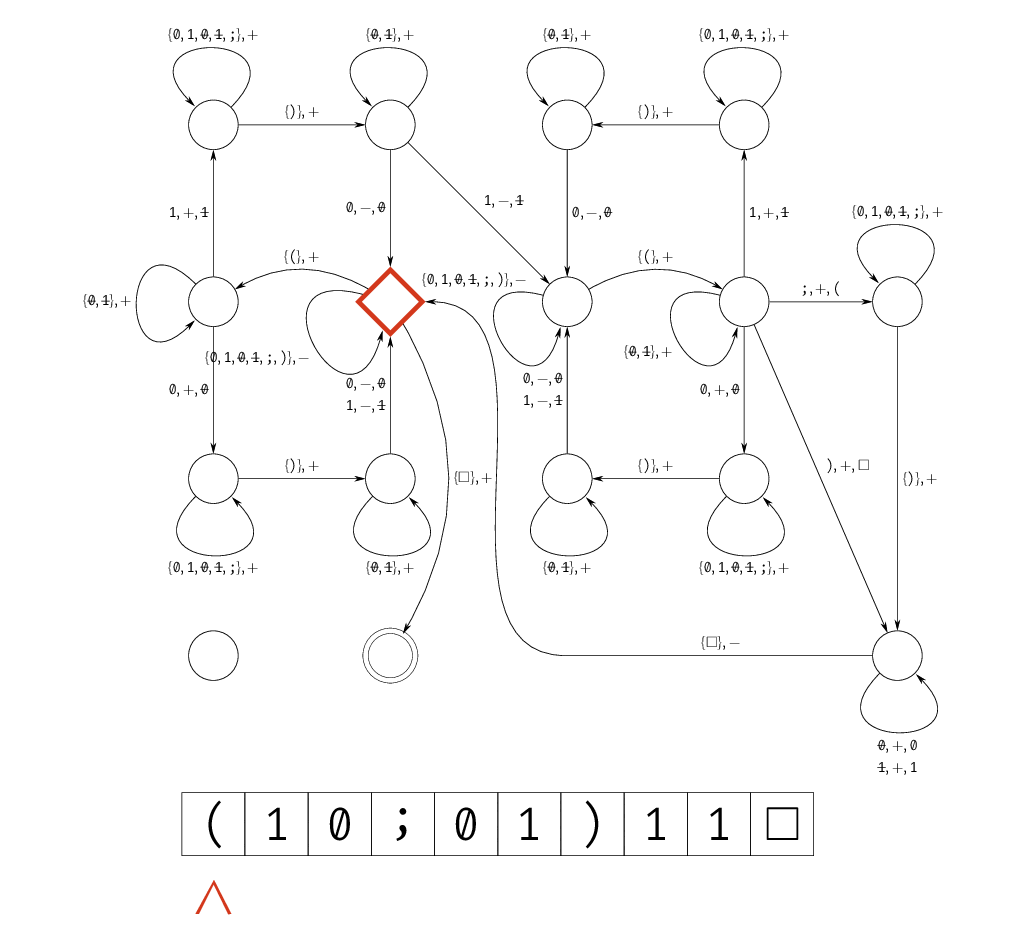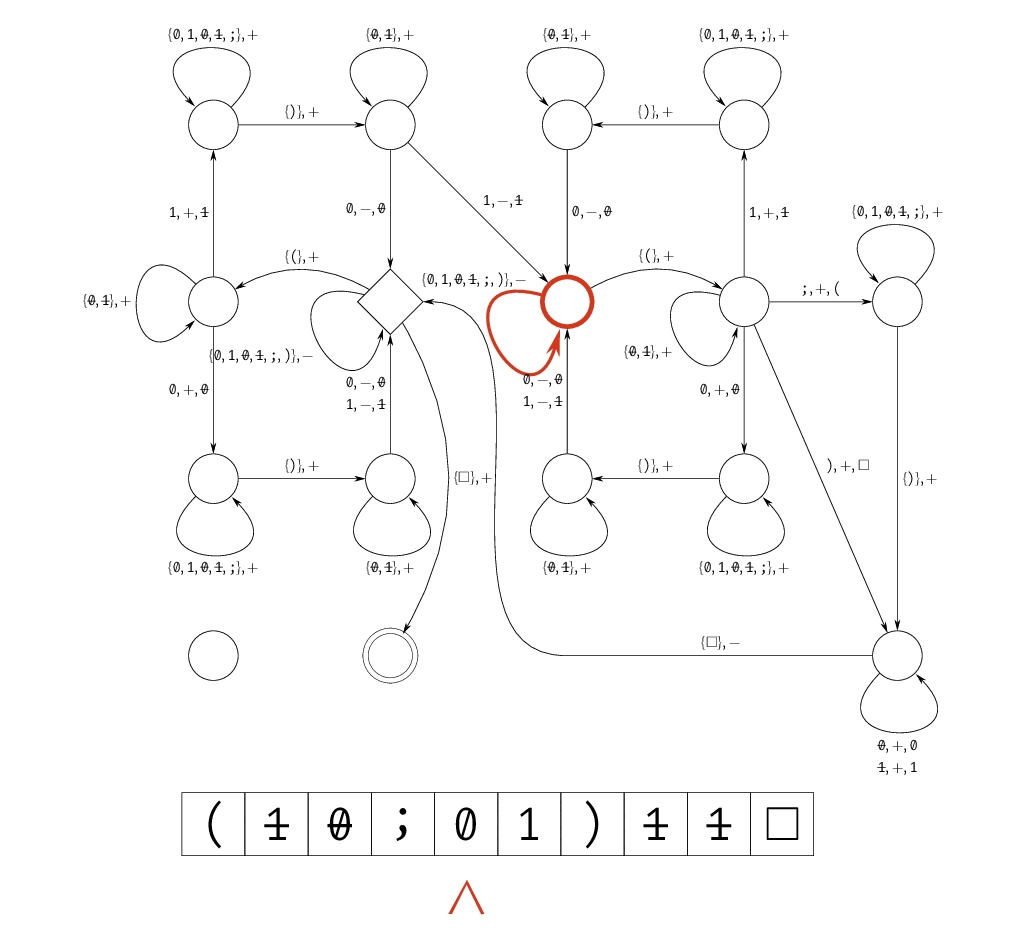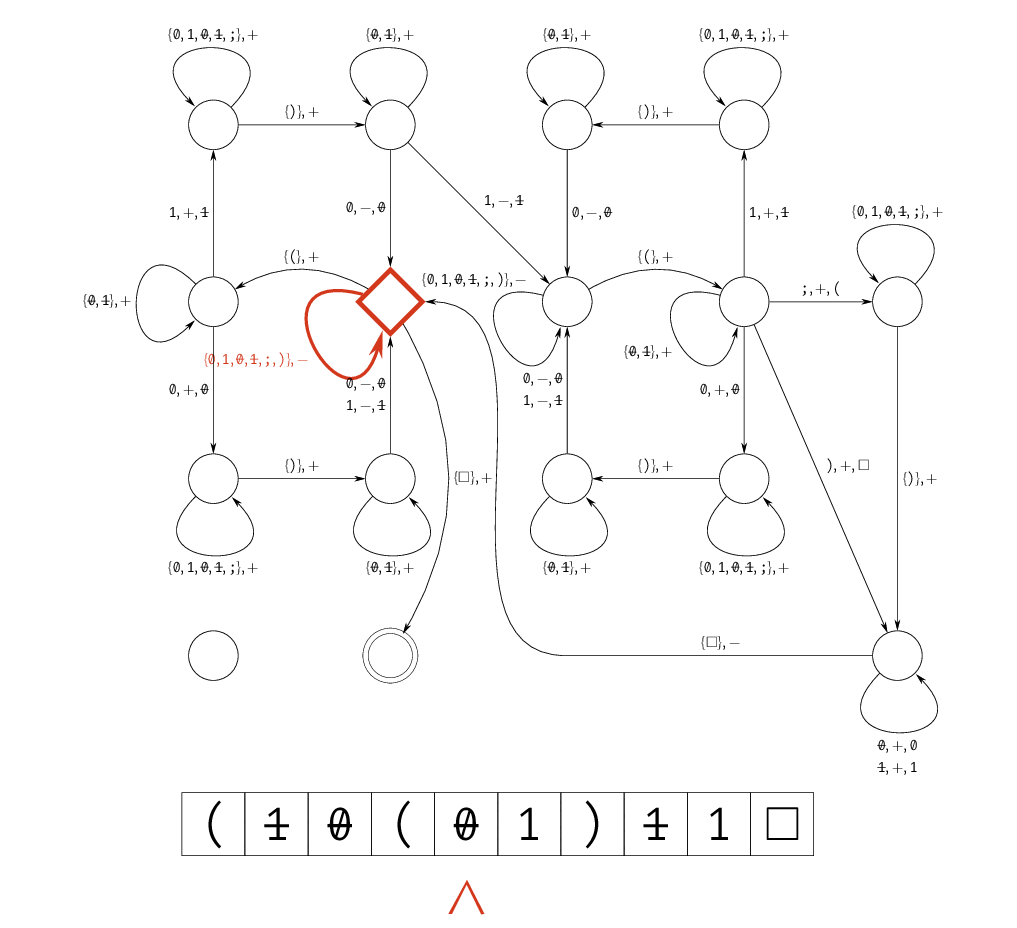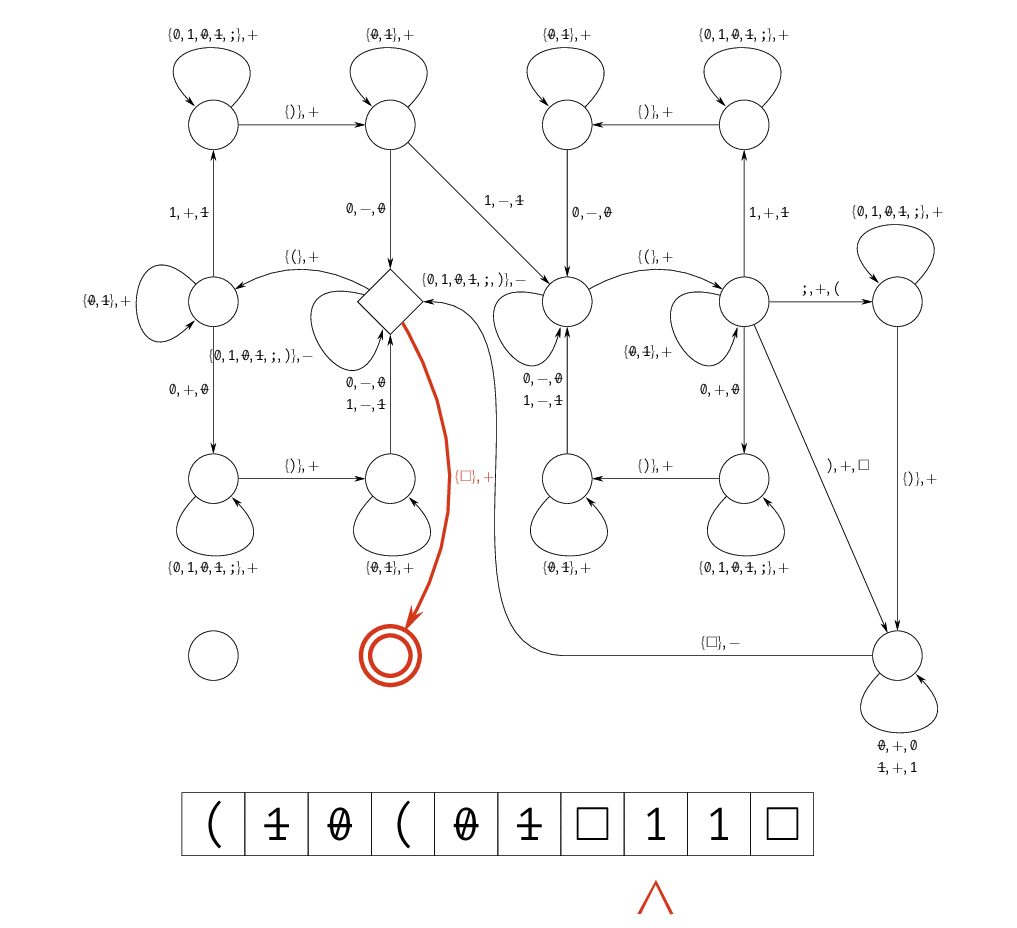
$\textstyle\left(\begin{smallmatrix}1&0\\0&1\end{smallmatrix}\right)\left(\begin{smallmatrix}1\\1\end{smallmatrix}\right)$ に対する動作

これを SAT に帰着させることを考えます。もちろん、ZOE を SAT に帰着させたいだけならもっと自然な方針がありますが、ここでは TM から帰着する例として行います。

境界条件の扱いなどで、Claim 1 で挙げた構成とは個数が必ずしも一致しませんが、下記のツイート群はそういうものでした。

今日の成果：854 変数、29359 節の SAT を解くことにより、1 * x = 1 の解が x = 1 であることがわかった
— えびちゃん🍑🍝🦃 (@rsk0315_h4x) 2025年7月21日

他にも、7844 変数、319980 節の SAT を解くことにより、1 * x + 0 * y = 1 かつ 1 * x + 1 * y = 1 が解 (x, y) = (1, 0) を持つことがわかった
— えびちゃん🍑🍝🦃 (@rsk0315_h4x) 2025年7月21日

40898 変数、1787769 節の SAT を 51 分かけて解き、0x+1y+1z = 1x+0y+1z = 1x+0y+0z = 1 が解 (x, y, z) = (1, 1, 0) を持つことがわかった
— えびちゃん🍑🍝🦃 (@rsk0315_h4x) 2025年7月21日

ZOE の入力として $A = \left(\begin{smallmatrix}1&0\\0&1\end{smallmatrix}\right)$ を与えるのは、$\angled{A} = \texttt{\char40}\texttt{10;01}\texttt{\char41}$ として $$ \begin{aligned} x_{0, 0, \texttt{\char40}}^{\text{symbol}} &= 1, & x_{0, 1, \texttt{1}}^{\text{symbol}} &= 1, & x_{0, 2, \texttt{0}}^{\text{symbol}} &= 1, & x_{0, 3, \texttt{;}}^{\text{symbol}} &= 1, \\ x_{0, 4, \texttt{0}}^{\text{symbol}} &= 1, & x_{0, 5, \texttt{1}}^{\text{symbol}} &= 1, & x_{0, 6, \texttt{\char41}}^{\text{symbol}} &= 1 \end{aligned} $$ に相当し、Claim 1 で示したように適切な変数・節を用いて SAT を解くことで、 $$ \begin{aligned} x_{0, 7, \texttt{1}}^{\text{symbol}} &= 1, & x_{0, 8, \texttt{1}}^{\text{symbol}} &= 1, & x_{0, 9, \blank}^{\text{symbol}} &= 1 \end{aligned} $$ が得られます。これにより、上記の検証器が $\texttt{\char40}\texttt{10;01\char41}\texttt{11}$ を受理することがわかります。すなわち、$\bm x=(1\; 1)$ がこの ZOE の certificate になることがわかります。

こうして、任意の $P = (I, O, \sigma)\in\NP$ に対して $\phi\in I$ が与えられたとき、$P$ に対する検証器 $D$ と $\phi$ を用いて SAT の問題例 $\theta$ を構成し、$\phi\in P_{\Yes}$ かどうかを判定できます。

$D$ は $\phi$ が与えられる前に固定されているものなので、$\angled{\phi}$ が長くなっても（計算ステップ数の意味で）気にすることはありません。 $D$ の状態の個数や遷移関数の定義域の要素数は $|\angled{\phi}|$ に対して定数ということです。よって、SAT のうち $D$ の状態遷移などに関わる部分は $|\angled{\phi}|^{O(1)}$ 個程度になります。どれだけ $D$ が複雑だったとしても（いわゆる）定数倍が大きくなるだけで、知ったことではないですね。

あとがき

有名問題であるところの Steiner Tree や Bin Packing などをやっていません。他にもいろいろあると思います。また、計算モデルとして、RAM や NTM なども触れていませんし、テープが複数本ある TM の話もしていません。そういえば 神託機械 (oracle machine) という概念もあります。

複雑性クラスにおいても、たとえば #P (number P) とか ⊕P (parity P) のようなものや、L とか PSPACE とか、他にもなんかいろいろなものがあるよ〜という話もあります。 strong NP-completeness の話とか、強多項式時間とか擬多項式時間とか、そういう話もありました。

そういえば、Complexity Zoo というものがあります。

complexityzoo.net

最近の 3Blue1Brown の動画で見覚えのあった人が zookeeper らしいです。

youtu.be

それから、久々に TikZ でいろいろおえかきをしました。ようやく \foreach をちゃんと使うようになったり、pgf にも興味を持ったりしました。

しかし、疲れたり飽きたりしてしまったので、一旦はここまでということにしちゃいます。各々が調べてくれたらうれしいです。

知らないまま生きているがお勉強したいとは思っていることリストを消化していきたいです。今回のトピックもその一つでした。浮動小数点数まわりはある程度なかよしになってきた気がします。乱数生成や暗号関連のトピックが気になり中です。正確には数ヶ月前の気になりトピックで最近は下火です。CTF の crypto をやれという話もあります。えびちゃん的には pwn や rev も好きなんだろうと思いますが、これも最近あまりできていませんね。

参考文献

CS103 のスライドや、岡本先生のスライドがおすすめだと思います。

おわり

おわってしまう。

*1:「その元問題から帰着した問題は該当の NP-complete の問題の特殊なケースになり、その場合は実は高速に解けます」とか、そういう状況もあるかもしれません。

*2:ここでは、$i\lt 0$ になっても拒否することにします。

*3:~~$\{i, j\}\in E$ の部分が well-defined ではない気がします。$i\le j$ などを仮定することによりよしなに定めるとします。~~ 気がしましたが気のせいでした。

*4:グラフの符号化というよりは、一般の 0/1 正方行列を整数として符号化する方式の話な気もします。正方とは限らない場合は $2^n 3^m \prod 5^{a_{i, j}\cdot(im+j)}$ みたいな感じでしょうか。

*5:定訳があるかはよくわかりませんでした。

*6:この $P$ は問題のことで、いわゆる $\P\ne\NP$ とかの $\P$ ではありません。

*7:非形式的な説明はよく言われがちですが、等価性はそこまで当たり前じゃない気がします。この記事では一旦 fact として扱い、今後の記事で別途考えます。

*8:充足可能という言い回し自体は、論理式全体に限らず、節に対して使うこともあります。

*9:高々 $3$ つとする問題設定もあります。後々 3-SAT から帰着することを考えると、3-SAT の形式が限定的である方が都合がよさそうなので、ちょうど $3$ つの方がうれしそうかも。

*10:$c(I_0) = c(\top)$ のとき、論理変数 $I_0$ が $\top$ であるというようなイメージで話しています。

*11:Independent Set の章で出した例とは異なるように選びました。

*12:実際には辞書順でなくとも適当な全順序を固定すればよさそう。