「そろそろ四則演算の誤差評価も飽きたな〜」「数学関数の計算とかもやってみてよ」という声が聞こえてきた*1ので、今日はそれをします。
導入
よく言われているような勘違いについて、一旦触れておきます。
cbrt(x)ってpow(x, 1.0/3.0)でよくない?
IEEE Std 754-2019 の 9.2.1 Special values には、下記の記述があります。
$\mathrm{pow}(x, y)$ signals the invalid operation exception for finite $x\lt 0$ and finite non-integer $y$.
実際、pow(-1.0, 1.0/3.0) を計算してみると、C では NaN になり、Python では ValueError: math domain error が出ました。
また、精度においても違いがあります。
1.0/3.0 というのは、$\tfrac13$ とは異なる値です。
$$
\begin{aligned}
1\oslash3
&= 0.{\small 333333333333333}{\footnotesize 314829616256247}{\scriptsize 390992939472198}{\tiny 486328125} \\
&= \tfrac13\cdot(1-2^{-54}).
\end{aligned}
$$
$\tfrac13\cdot 2^{-54}$ の誤差のせいで、(cbrt が correctly-rounded な値を返すとして実装されていたとしても)所望の値になってくれないケースがしばしば発生します。
$$
\begin{aligned}
64^{\tfrac13\cdot(1-2^{-54})}
&= 3.{\small 999999999999999}{\footnotesize 692180816275335}{\scriptsize 216604455276753}{\tiny 748400773143551{\dots}}, \\
\roundp{64^{\tfrac13\cdot(1-2^{-54})}}
&= 3.{\small 999999999999999}{\footnotesize 555910790149937}{\scriptsize 383830547332763}{\tiny 671875} \\
&= 4-2^{-51}.
\end{aligned}
$$
そういうわけで、専用の関数を使う必要があるわけですね。
note: 1.0 / 3.0 を渡された pow 関数側に「オッ cbrt を計算したいんやな、気ィ利かせて補正しといたろw」とされると、それはそれでめちゃくちゃになりますね*2。
glibc 実装
精度?
cbrt(3375.0) を計算してみると、14.9999999999999982236431605997495353221893310546875 になりました。ウ〜ンム。
$3375 = 15^3$ ですが、$15-2^{-49}$ が返ってきていて嫌な気持ちになりますね。
note: GCC で単に cbrt(3375.0) と書くと 15.0 が出力される場合がありますが、これはコンパイル時に計算しているためです(アセンブリを見たりするとわかります)。C の規格的には、コンパイル時の計算と実行時の計算で精度などに違いがあることは許容されています。cbrt(strtod("3375", NULL)) などとすると、そういう最適化を防げそうです。それでも防げなかった場合は、実行時に与えるようにするとよいですね。
N2347 からの引用
6.6/5
An expression that evaluates to a constant is required in several contexts. If a floating expression is evaluated in the translation environment, the arithmetic range and precision shall be at least as great as if the expression were being evaluated in the execution environment.
5.2.4.2.2/8
The accuracy of the floating-point operations (
+,-,*,/) and of the library functions in<math.h>and<complex.h>that return floating-point resuls is implementation-defined, as is the accuracy of the conversion between floating-point internal representations and string representations performed by the library functions in<stdio.h>,<stdlib.h>, and<wchar.h>. The implementation may state that the accuracy is unknown.
そんな無責任なあ。$\eod$
19.7 Known Maximum Errors in Math Functions には、glibc が correct rounding な結果を目指しているわけではない旨や、crsin のように correct rounding 版を用意するかもしれない旨や、既知の誤差の表などが記載されています。
note: GCC (the GNU Compiler Collection) と glibc (the GNU C Library) は別物で、こうした標準関数は GCC ではなく glibc が提供しているものです。GCC はあくまで、(別途用意されているところの)glibc の関数を呼び出す実行ファイルを作っているだけですね (cf. 4.14 Library Functions)。
まえおき
さて、correctly-rounded ではないと知ってやる気を失くしている人もいるかもしれませんが、一応実装を見に行きましょう。 読者の人々(や、昔のえびちゃん)は数値計算のアルゴリズムに明るくないので、「どうせ Taylor 展開とかをしてるんでしょ?」のようなぼやぼやっとしたイメージをしていることと思いますが、そうではないです。
sysdeps/ieee754/dbl-64/s_cbrt.c (glibc-2.41) を読んでいきます。
disclaimer: sysdeps 配下の構造をいまいちわかっていないです。また、数学関数のライブラリのファイル名には e_ k_ s_ t_ v_ w_ などの prefix がついているのですが、これがなにを意味するのかもわかっていないです。glibc 以外の数学関数のライブラリでもこうした名前になっており、そうした慣習がある(or 昔のえらいプロジェクトがそうしていた?)とかなのかなぁと思っています。w_ は wrapper なのかなという雰囲気は感じています。k_ は kernel を意味していそうなのを見た記憶はあります*3。
方針
大まかな方針は次の通りです。
$\gdef\quot{\operatorname{quot}}$ $\gdef\rem{\operatorname{rem}}$
- ${|x|} = x_m\times 2^{x_e}$ として分解する。ここで、$x_m\in[0.5\lldot 1)$ で、$x_e$ は整数である。
- $\sqrt[3]{|x|} = x_m^{1/3}\times 2^{x_e/3} = (x_m^{1/3}\cdot 2^{(x_e\rem 3)/3})\times 2^{x_e \quot 3}$ と変形し、それぞれの部分を求める。
- $\quot$ と $\rem$ はそれぞれ C の
/と%に対応する除算と剰余算。商を $0$ 方向に丸めるため、あまりが負になることもある。
- $\quot$ と $\rem$ はそれぞれ C の
$(x_m, x_e)$ を求める部分は、frexp という標準関数によって行います。これは、内部のビット表現の操作によるものなので、誤差なしで可能です。
この際に、$0_{\pm}$, $\pm\infty$ や NaN であることの判定も可能なので、それらの場合はそのまま返してしまいます。
定数の計算
さて、本題となる下記について考えていきます。 $$ \sqrt[3]{|x|} = (x_m^{1/3}\cdot 2^{(x_e\rem 3)/3})\times 2^{x_e \quot 3}. $$ まず、$2^{(x_e\rem 3)/3}$ の部分は $2^{-2/3}$, $2^{-1/3}$, $2^{0/3}$, $2^{1/3}$, $2^{2/3}$ の 5 通りしかないため、定数として用意しておきます。 $$ \begin{aligned} r_{-2} &= 0.{\small 629960524947436}{\footnotesize 484310969717625}{\scriptsize 994235277175903}{\tiny 3203125}, \\ r_{-1} &= 0.{\small 793700525984099}{\footnotesize 680698591328109}{\scriptsize 614551067352294}{\tiny 921875}, \\ r_0 &= 1, \\ r_1 &= 1.{\small 259921049894873}{\footnotesize 190666544360283}{\scriptsize 296555280685424}{\tiny 8046875}, \\ r_2 &= 1.{\small 587401051968199}{\footnotesize 583441787581250}{\scriptsize 537186861038208}{\tiny 0078125}. \end{aligned} $$
$\angled{r_1, r_2} = \angled{\roundp{\sqrt[3]{2}}, \roundp{\sqrt[3]{4}}}$ ですが、$\angled{r_{-2}, r_{-1}} = \angled{1\oslash r_2, 1\oslash r_1} \ne \angled{\roundp{\sqrt[3]{0.25}}, \roundp{\sqrt[3]{0.5}}}$ となっています。
これらの値に関して
sysdeps/i386/fpu/s_cbrt.S でも同様のアルゴリズムがアセンブリで書かれていますが、こちらでは $\angled{r_{-2}, r_{-1}} = \angled{\roundp{\sqrt[3]{0.25}}, \roundp{\sqrt[3]{0.5}}}$ となっており、意図した定義になっているのかは微妙な気がします。コンパイル時計算などで実は correctly-rounded の値になる可能性も否定はできませんが、手元の環境ではそうはなっていないようでした。
volatile double x = 0.125; // コンパイル時に計算されるのを防ぐ cbrt(x);
として、$0.5$ になれば $r_{-2} = \roundp{\sqrt[3]{0.25}}$ となっています。
volatile double x = 0.25; cbrt(x);
こちらは、$0.{\small 629960524947436}{\footnotesize 706355574642657}{\scriptsize 302320003509521}{\tiny 484375}$ になれば $r_{-1} = \roundp{\sqrt[3]{0.5}}$ となっています。なお、このときの cbrt(0.25) の値は $\roundp{\sqrt[3]{0.25}}$ とは異なっていることに注意してください 🥲。
$$ \begin{aligned} \roundp{\sqrt[3]{0.5}} &= 0.{\small 793700525984099}{\footnotesize 791720893790625}{\scriptsize 268593430519104}{\tiny 00390625}, \\ \roundp{\sqrt[3]{0.25}} &= 0.{\small 629960524947436}{\footnotesize 595333272180141}{\scriptsize 648277640342712}{\tiny 40234375}. \quad\eod \end{aligned} $$
近似多項式
さて、残りは $x_m^{1/3}$ を求めるパートです。 定義から $x_m\in[0.5\lldot1)$ です。 このように、入力が特定の区間に含まれるケースに帰着する手法は、これ以外の数学関数においてもしばしば見られます。
以下で定義される多項式 $f$ を考えます。 $$ \begin{aligned} f(x) &= 0.{\small 354895765043919}{\footnotesize 841907893442112}{\scriptsize 253978848457336}{\tiny 42578125} \\ &\qquad {}+ 1.{\small 508191937815849}{\footnotesize 037463067361386}{\scriptsize 492848396301269}{\tiny 53125}\,x \\ &\qquad {}- 2.{\small 114994941673713}{\footnotesize 046981220031739}{\scriptsize 212572574615478}{\tiny 515625}\,x^2 \\ &\qquad {}+ 2.{\small 446931225635344}{\footnotesize 375746171863283}{\scriptsize 962011337280273}{\tiny 4375}\,x^3 \\ &\qquad {}- 1.{\small 834692774836130}{\footnotesize 801929812150774}{\scriptsize 523615837097167}{\tiny 96875}\,x^4 \\ &\qquad {}+ 0.{\small 784932344976639}{\footnotesize 218003811038215}{\scriptsize 644657611846923}{\tiny 828125}\,x^5 \\ &\qquad {}- 0.{\small 145263899385486}{\footnotesize 366933051272098}{\scriptsize 964545875787734}{\tiny 9853515625}\,x^6. \end{aligned} $$
この $f$ に対して $x_m^{1/3} \approx f(x_m)$ が成り立ちます。 $f(x_m)$ の計算の際には Horner’s method を用います*4。$f$ の計算にも誤差が出るため、Horner’s method による $f(x_m)$ の値は $\hat f(x_m)$ と表記することにしましょう。
この多項式は、おそらくは Remez algorithm などで求めたのだろうと推測しています。特定の区間における誤差の最大値を最小化するような(予め決めた次数以下の)近似多項式を求めるアルゴリズムです。 $x_m\in[0.5\lldot 1)$ としているので、$[0.5\lldot 1)$ でのよい近似が得られていればよいですね。
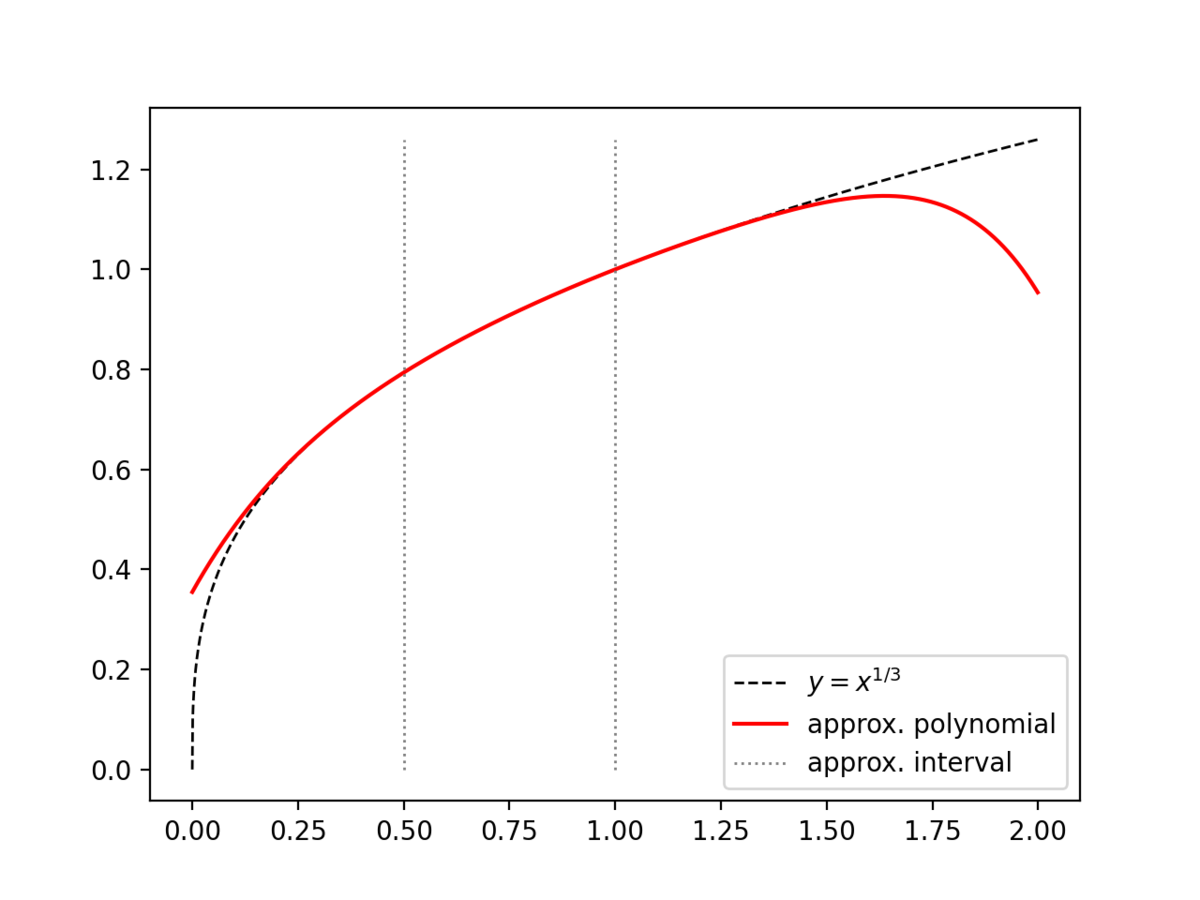
点線がその境界、破線が近似されるべき真の値 $y=x^{1/3}$ で、赤の実線が上記の多項式 $y=\hat f(x)$ です。よさそうな見た目をしていますね。
念のためもう少し近づけておく
$\gdef\signum{\operatorname{sgn}}$
さて、もう少しだけ続きます。$\signum(x)\times(\hat f(x_m)\otimes r_{x_e\rem 3})\times 2^{x_e\quot 3}$ を返すわけではないです。
返すのは、$u = \hat f(x_m)$ および $t_2 = u\otimes u\otimes u$ として、次の値です。 $$ \signum(x)\times (u \otimes (t_2 \oplus 2x_m)\oslash(2t_2\oplus x_m)\otimes r_{x_e\rem 3})\times 2^{x_e\quot 3} $$
やっぱり $\circledast$ の表記だと分数が使えないので読みにくい 🥲。 計算せんとしている式の絶対値は次の通りです($\signum(x)$ の部分は煩雑になるので省きたいです)。 $$ u\cdot\frac{u^3+2x_m}{2u^3+x_m}\cdot r_{x_e\rem 3}\times 2^{x_e\quot 3} $$
$u \xgets{\times} \tfrac{u^3+2x_m}{2u^3+x_m}$ で更新し、$u\cdot r_{x_e\rem 3}\times 2^{x_e\quot 3}$ を返そうとしているという見方もできます。というわけで、この更新について見ていきます。
これは、Newton’s method ではなく Halley’s method と呼ばれる反復アルゴリズムの更新ステップです。次のような更新をします。 $$ x_{n+1} = x_n - \frac{2g(x_n)g'(x_n)}{2g'(x_n)^2-g(x_n)g''(x_n)} $$ この反復により、$g(x) = 0$ の根を求めます。 たとえば $a$ の 3 乗根を求めたいときは $g(x) = x^3-a$ として行えばよいですね。 $g'(x) = 3x^2$, $g''(x) = 6x$ です。
$$ \begin{aligned} x_{n+1} &= x_n - \frac{2\cdot(x_n^3-a)\cdot 3x_n^2}{2\cdot(3x_n^2)^2-(x_n^3-a)\cdot 6x_n} \\ &= x_n - \frac{6x_n^5 - 6ax_n^2}{18x_n^4 - 6x_n^4+6ax_n} \\ &= x_n - \frac{x_n^4 - ax}{2x_n^3+a} \\ &= \frac{2x_n^4+ax_n-x^4+ax_n}{2x_n^3+a} \\ &= x_n\cdot \frac{x_n^3+2a}{2x_n^3+a} \end{aligned} $$ $(x_n, a) = (u, x_m)$ とすることで、上で見た式と一致します。
$u^3$ を t2 という名前にした意図はよくわかりませんでした。何らかの一般的な手法で使われていた記号を流用したとかでしょうか。
完成
$\signum(x)\times u\cdot r_{x_e\rem 3}\times 2^{x_e\quot 3}$ を返します。
最後の $2^{x_e\quot 3}$ を掛けるパートは、ldexp という標準関数により行います。
余談
だったら $f$ なんて使わずに最初から Halley’s method を使えばいいんじゃんという声も聞こえます。 おそらくは除算が重いため避けているのではないかなと推測するところです。
(xm, xe) = math.frexp(x) yi = math.ldexp(xm, xe // 3) for _ in range(4): yi3 = yi * yi * yi yi *= (yi3 + 2 * xi) / (2 * yi3 + xi) # yi3 = yi * yi * yi # yi3_xi = yi3 + xi # yi *= (yi3_xi + xi) / (yi3_xi + yi3)
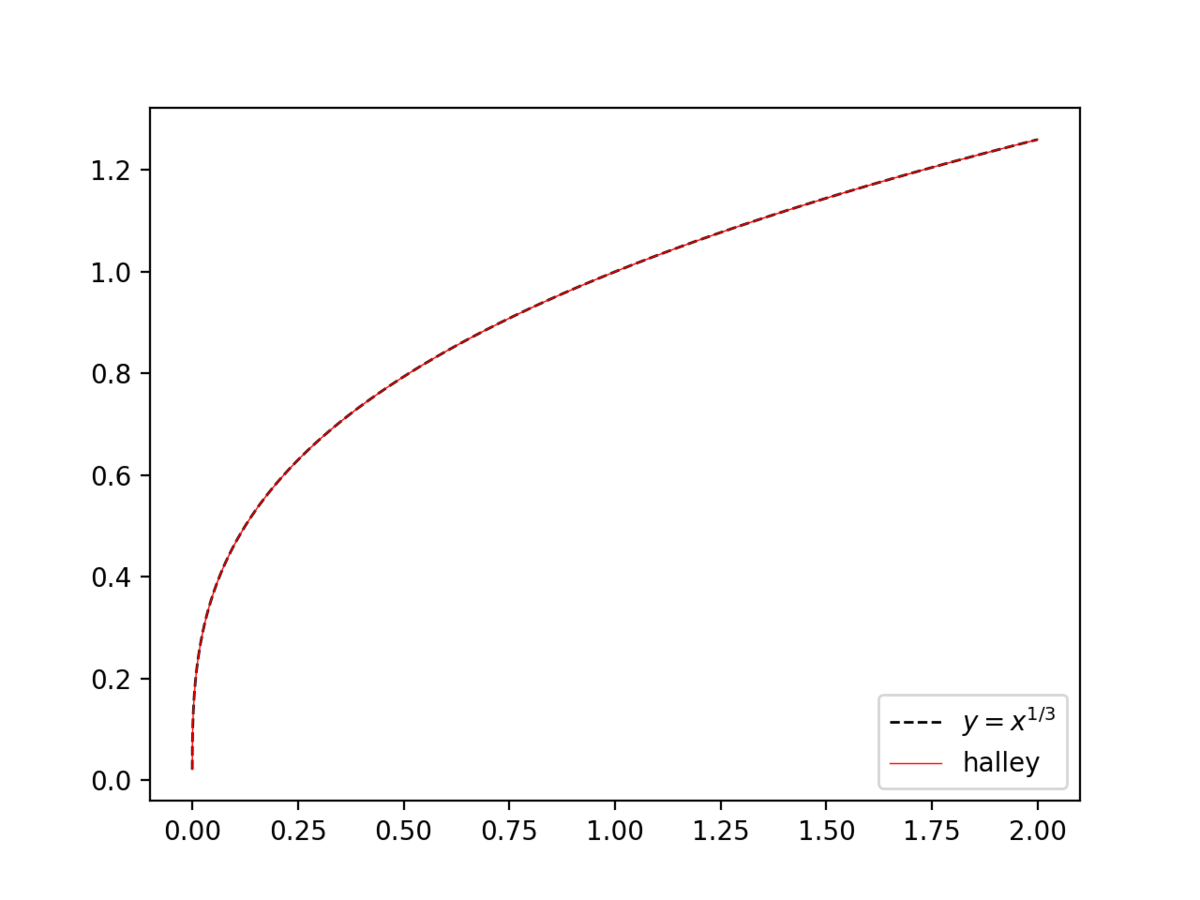
$(0\lldot 2]$ の範囲で $10^{-5}$ 刻みで試したところ、4 回の反復でだいたい $5\times 10^{-16}$ 程度の相対誤差に収まっていそうでした。 反復が 3 回のときは $6\times 10^{-6}$ くらいでした。3 次収束らしいので、1 回の反復でだいぶ差が出ますね。
反復 1 回あたり +, *, / がそれぞれ 2, 5, 1 回(計算順序を変えて yi3 + xm 先に計算することにしても 3, 3, 1 回)です。
Horner’s method による $\hat f$ の計算回数はそれぞれ 6, 6, 0 回(- も + として計上)なので、Halley’s method 2 回分よりもお得ですね。適当な初期値から反復するよりも、多項式を用いて計算する方がお得です。
Halley’s method で収束した後の値に対して $r_{x_e\rem 3}$ を掛けるのは、損しているような気がしないでもないような気もします。
また、Newton’s method で yi *= (2 * yi3 + xi) / (3 * yi3) を用いた場合は、反復を 7 回しても $4\times 10^{-12}$ 程度の誤差がありました。
参考文献
感想
今回は glibc の cbrt を見ましょうというだけの回でしたが、やっぱりそれだけじゃ満足できなくて、(使い道がどの程度あるかなんてのはさておき)correctly-rounded な値を計算できることに憧れますよね。
競プロ界隈においては(というか人間界においては)、「そんな標準関数の精度を気にするより、普通の四則演算で catastrophic cancellation を起こさないように気をつける方が先ですよ」というケースの方が多いので、correctly-rounded なんてのはまだ先の先の話かもしれないですが、人間界の事情なんてえびちゃんの知ったことではないですね。
近似多項式 $f$ も天下りで与えたものを使っただけなので、ちょっと物足りなさはあります。 Remez algorithm についても深掘りできたらいいなと思っています。
C や IEEE 754、POSIX に C++ と、さまざまな規格で思い思いの数学関数を定義しておられるので、めちゃくちゃな個数の数学関数があります。特に C++ はもうめちゃくちゃです。
数学関数たち
C の規格で定義されている数学関数には下記があります。ビット操作やそれに類するものなどは除外しています。
- trigonometric functions
- hyperbolic functions
acosh$\arcosh(x)$,asinh$\arsinh(x)$,atanh$\artanh(x)$
- exponential and logarithmic functions
exp$e^x$,exp2$2^x$,expm1$e^x-1$log$\ln(x)$,log10$\log_{10}(x)$,log1p$\ln(1+x)$,log2$\log_2(x)$
- power and absolute-value functions
cbrt$x^{1/3}$fabs$|x|$hypot$\sqrt{x^2+y^2}$pow$x^y$sqrt$\sqrt x$
- error and gamma functions
erf$\operatorname{erf}(x) = \displaystyle\frac2{\sqrt\pi}\int_0^x e^{-t^2}\,\mathrm{d}t$erfc$\operatorname{erfc}(x) = 1 - \operatorname{erf}(x)$lgamma$\ln(|\Gamma(x)|)$tgamma$\Gamma(x)$
- nearest integer functions
ceil$\ceil{x}$floor$\floor{x}$round,roundeven,trunc
- floating multiply-add
fma$(x\times y)+z$
IEEE Std 754-2019 の additional mathematical operations には、下記のような関数もあります。
exp2m1$2^x-1$,exp10$10^x$,exp10m1$10^x-1$log2p1$\log_2(1+x)$,log10p1$\log_{10}(1+x)$rSqrt$1/\sqrt{x}$compound$(1+x)^n$rootn$x^{1/n}$sinPi$\sin(\pi x)$,cosPi$\cos(\pi x)$,tanPi$\tan(\pi x)$asinPi$\arcsin(x)/\pi$,acosPi$\arccos(x)/\pi$,atanPi$\arctan(x)/\pi$atan2Pi
POSIX には次の関数もあります。
C++ にもたくさんあります (cf. [cmath.syn])。列挙を諦めました。ところでこれいつ使うんですか? $\eod$
え、これ全部の correctly-rounded 版を実装させられるんですか...? 😭(correctly-rounded の本質は、実装ではなく証明パートという話もあります。)
おわり
おわりです。
*1:自分の中から聞こえてきた声です。そもそも浮動小数点型に興味を持っているフォロヮが少ないため。
*2:現実としては、そういうめちゃくちゃな使い方をしたい人が多そうなので、そういう仕様の方が「幸福度」が高くなるのかもしれませんが...。そういう ad hoc な意味不明仕様にはなってほしくないですね。
*3:たぶん Linux kernel とかの kernel とは違う文脈で、「核となる部分だよ〜」くらいだと解釈しています。
*4:$a_0+a_1x+a_2x^2+\cdots$ を計算する際に、$a_0\oplus (a_1\otimes x)\oplus(a_2\otimes x\otimes x) \oplus \cdots$ とするのではなく、$( (\cdots\oplus a_2)\otimes x\oplus a_1)\otimes x\oplus a_0$ とする手法。